Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 95
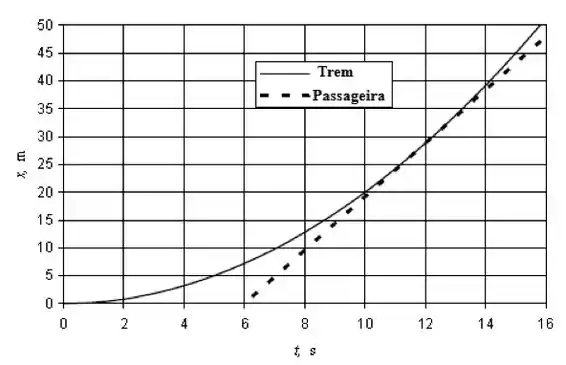
Um trem parte de uma estação com uma aceleração constante de 0,40 m/s². Uma passageira chega a um ponto junto ao trilho 6,0 s após o final do trem ter passado pelo mesmo ponto. Qual é a menor rapidez constante com que ela deve correr para ainda alcançar o trem? Em um único gráfico, plote as curvas posição versus tempo para o trem e a passageira.
Passo 1
Nesse problema a gente tem um trem e trens costumam ser beeeem grandes! Certo? Mas como o problema não fala o comprimento do trem a gente vai considerar ele desprezível! Beleza?!
Com isso em mente, vamos ver o que o problema fala:
O trem sai da posição no tempo com uma aceleração constante de . Mas a passageira só chega na posição quando .
Vamos chamar de “crítico” o momento em que a passageira alcança o trem. Então isso acontece em , neste momento a passageira esta com em e o trem tem e esta em .
Mas se a gente ta falando que a passageira vai alcaçar o trem, logo:
Vamos imaginar o momento que a passageira encontra o trem como um espaço infinitesimal, naquele momento critico tanto a passageira quanto o trem percorrem esse mesmo espaço pequenininho em um mesmo tempo.
Olhando a definição de velocidade instântanea:
Logo:
O trem esta em um movimento acelerado e pode ser escrito como:
Já para a passageira:
Passo 2
Se a gente parar pra pensar o que tem que acontecer para a passageira encontrar o trem é que ela tem que correr a mesma distância que o trem mas ela tem que fazer isso usando a menos.
Se a gente igualar as equações de posição que vimos no Passo 1, não vamos chegar em lugar nenhum, pois temos as informações necessárias.
O que a gente pode fazer é escrever a velocidade média do trem:
Mas se a aceleração é constante, também podemos dizer que a é a média da sua velocidade inicial e final, certo?
Agora podemos igualar as duas expressões :
Isolando :
Igualando a expressão para que escrevemos no Passo 1:
A passageira só vai alcançar o trem se ela estiver na mesma velocidade que ele, logo:
Então fazemos:
Arrumando:
Para
Passo 3
Agora que a gente conhece , podemos calcular :
Só relembrando que e :
Finalmente:
Uhuuuuul!!!
Passo 4
Agora temos que plotar as curvas da posição em função do tempo, para isso temos:
Substituindo os valores:
Ficamos com:
Já para a passageira:
Substituindo e :
Arrumando:
Agora é só plotar o gráfico! Ele fica assim:
