Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.Problemas - Ex. 61

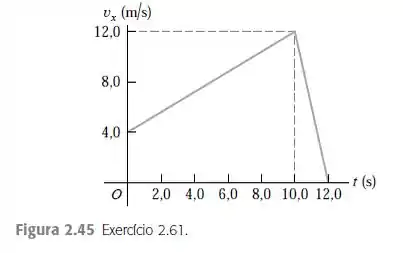
Uma gazela está correndo em linha reta ( o   e i x o   x ). O gráfico na Figura 2.45 mostra a velocidade desse animal em função do tempo. Nos primeiros 12,0   s , determine a) A distância

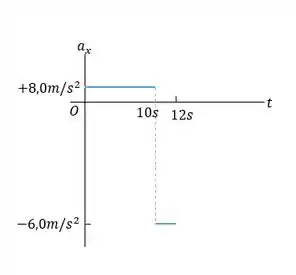
total percorrida e b) O deslocamento da gazela. c) Faça um gráfico a x t demonstrando a aceleração desse animal em função do tempo para os primeiros 12,0   s .

Passo 1

Vamos analisar o gráfico da figura 2.45:

Quando o gráfico da velocidade versus o tempo é uma linha reta, a aceleração é constante, então podemos que observar que o movimento da gazela consiste em dois trechos de aceleração contante. Então nós vamos aplicar as equações da aceleração para cada um desses trechos.

Vamos analisar os trechos:

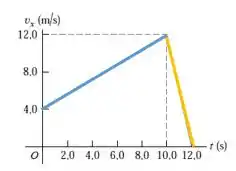
Em azul, temos o movimento sempre positivo, na direção + x e a distância total movida é igual a magnitude do deslocamento. Do instante de tempo t = 0   até t = 10 s a velocidade inicial, v 0 = 4 m / s e a velocidade final, v = 12 m / s .

Em amarelo, o movimento temos a aceleração em declínio, ou seja, uma desaceleração. Nos instantes de tempo t = 10 s a t = 12 s a velocidade inicial v 0 = 12 m / s e a velocidade final, v = 0 .

Passo 2

  1. Para o intervalo de tempo t = 0 a t = 10 s , vamos calcular a posição x 1 :

    2. ∆ t = 10 s - 0 = 10 s

    x 1 = v 0 + v 2 t = 4   m/s + 12   m/s 2 ⋅ 10   s

    x 1 = 80   m  

    Para o intervalo de tempo t = 10   s a t = 12   s , vamos calcular a posição x 2 :

    ∆ t = 12   s - 10   s

    ∆ t = 2   s

    Logo:

    x 2 = v 0 + v 2 t

    x 2 = 12   m/s + 0 2 ⋅ 2   s

    x 2 = 12   m

    Passo 3

  2. Para encontrarmos a distância total x basta fazer a soma dos dois trechos:

    3. x = x 1 + x 2

    x = 80   m + 12   m

    x = 92   m

    Passo 4

  3. Então, vamos encontrar a aceleração para os dois trechos:

a = v f i n a l - v i n i c i a l t

Para o intervalo de tempo t = 0 a t = 10 s :

a = 12 m / s - 4 m / s 10 s = 0,800 m / s 2

Para o intervalo de tempo t = 10 s a t = 12 s :

a = 0 m / s - 12 m / s 2 s = - 6 m / s 2

Quando a velocidade e a aceleração são positivos, a velocidade aumenta.

Quando a velocidade é positiva e a aceleração é negativa, a velocidade diminui.

Resposta

  1. 92   m
  2. 92   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Astronautas, em um planeta distante, lançam uma pedra no ar. Com o auxílio de uma câmara que tira fotos a uma taxa constante, eles registram a altura da rocha como uma função do tempo, como dado na ta
Esboce gráficos da velocidade e da aceleração, em função do tempo, do corpo cujo movimento é mostrado na figura 2.16.
Em seu laboratório de física, você solta um pequeno planador a partir do repouso em diversos pontos em uma rota aérea longa, sem atrito, que está inclinada em um ângulo u acima da horizontal. Com uma
Conforme um corpo se move ao longo do eixo x, várias medições da sua posição são realizadas, o suficiente para gerar um gráfico suave e preciso de xv e r s u st . Qual das seguintes quantidades para o
Quando uma bola de futebol é chutada na direção de um jogador e o jogador desvia de cabeça, a aceleração da cabeça durante a colisão pode ser relativamente grande. A Fig 2-35 mostra a aceleração a ( t