12.50. Uma esfera uniforme de massa igual a 60,0 kg é mantida fixa com seu centro na origem e uma segunda esfera uniforme de massa igual a 80,0 kg é mantida fixa com seu centro no ponto x=0, y=3,0m. a) Determine o módulo, a direção e o sentido da força gravitacional resultante produzida por essas esferas sobre uma terceira esfera uniforme com massa igual a 0,500 kg situada no ponto x=4,0m , y=0. b) Em que ponto, sem ser o infinito, a terceira esfera deve ser colocada para que a força gravitacional resultante que atua sobre ela seja igual a zero?
Passo 1
Vamos começar resolvendo o item (a). O enunciado descreve a seguinte situação
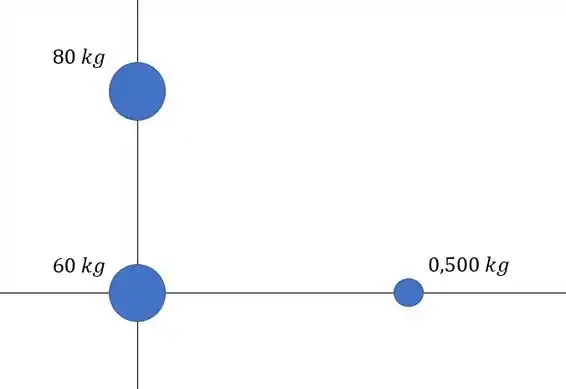
Bom, a gente vai ter essas forças agindo no sistema

Tudo que a gente precisa fazer é calcular as forças e somar vetorialmente.
Passo 2
Podemos calcular o módulo da força gravitacional assim
Vamos começar calculando
A distância é 4 porque a massa maior está em e a menor em .
Isso vai dar
Agora vamos calcular . Mas vamos calcular decompondo nas coordenadas
Substituindo os valores
E isso vai dar
Agora podemos calcular a força total
Isso vai dar
Passo 3
Agora que temos a força em notação vetorial, podemos conseguir tudo que o exercício pede: Módulo sentido e direção.
Vamos começar com o módulo
Isso vai dar
Agora vamos calcular a direção. Bem a gente pode calcular um vetor unitário que aponta na direção da força resultante
Ou seja
E isso vai dar
E pela imagem a gente pode ver que o sentido do vetor aponta para entre as massas.
Passo 4
Vamos finalmente para o item (b). A gente quer saber em qual ponto a gente pode colocar a terceira massa para que a força resultante sobre ela seja 0. Em outras palavras, a força gravitacional que a massa de 60 kg exercer sobre a terceira massa tem que ter mesmo módulo, mas sentido contrário, a força gravitacional que a massa de 80 kg vai exercer sobre a terceira massa. Então
Bom, a gente já pode começar cortando .
Então
Ou ainda
Beleza, o que temos aqui é uma equação com duas incógnitas. Para descobrir essas incógnitas precisamos de pelo menos mais uma equação. A gente pode achar essa outra equação se a gente assumir que a terceira massa tem que estar em algum lugar entre as duas primeiras. Essa vai ser a única configuração possível onde as forças que as massas exercem sobre a terceira massa não se somam, mas se cancelam. Assim as distâncias tem que ser igual a distância entre as duas massas, que no caso é .
Então chegamos na equação
Agora a gente consegue resolver. Basta fazer
Isso vai dar
Substituindo os valores
Então
Logo
Então a terceira massa tem que ser colocada na linha que une as duas outras massas, a uma distância de da massa de e da massa de .
Resposta
-
Modulo:
Direção:
Sentido: Aponta para entre as massas.
- A terceira massa tem que ser colocada na linha que une as duas outras massas, a uma distância de da massa de e da massa de .