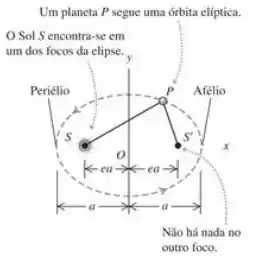
12.35. a) Use a Figura 12.19 para mostrar que a distância entre o Sol e um planeta no periélio é igual a , e a distância entre o Sol e um planeta no afélio é igual a e, portanto, a soma dessas duas distâncias é igual a 2a . b) Plutão é chamado de planeta externo, porém, durante o periélio em 1989 ele estava quase 100 milhões de quilômetros mais perto do Sol do que Netuno. Os semi-eixos maiores das órbitas de Plutão e de Netuno são respectivamente, e , e as respectivas excentricidades são 0,248 e 0,010. Ache a menor distância entre o Sol e Plutão e a maior distância entre o Sol e Netuno. C) Depois de quantos anos do periélio de Plutão em 1989 Plutão estará novamente no periélio?
Passo 1
Legal, vou começar fazendo um desenho da figura 12.19 destacando os pontos que a gente vai precisar
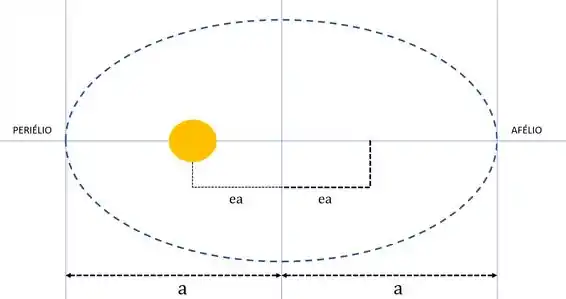
Agora repare que no ponto do periélio, a distância até o sol é , então
A gente coloca o em evidência e temos
Agora vamos fazer a distância até o afélio. Repare que nesse caso a gente tem
A gente coloca o em evidência
Agora vamos ver quanto dá a soma dessas duas distâncias
A gente pode colocar o em evidência de novo
Bem isso vai dar
Exatamente como queríamos demonstrar.
Passo 2
Agora vamos para o item (b). Vamos começar achando a menor distância entre Sol e Plutão, que vai acontecer justamente no periélio de plutão.
Bom como vimos no item anterior, o periélio teme essa distância
O exercício nos dá o semieixo e a excentricidade, é só a gente substituir
Agora fazendo essas contas a gente tem
Agora vamos ver a maior distância que Netuno pode ficar do Sol. Isso vai acontecer no afélio, então a gente pode calcular essa distância assim
Substituindo os valores que o enunciado dá
Fazendo essa continha
E aí temos
E esse é o item (b)
Passo 3
Agora vamos para o item final. A gente tem que dizer quanto tempo vai levar para Plutão voltar ao periélio, ou seja, a gente tem que calcular o período. E para isso a gente pode usar a terceira lei de Kepler
O enunciado nos dá o eixo maior, a constante gravitacional e a massa do Sol a gente pode encontrar no Apêndice do livro. Então é só substituir os valores
Agora é só fazer essa continha
Vamos passar isso para dias
Ainda deu um número muito grande :/. Vamos colocar em anos então
Resposta
b)
c)