Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Exercício - Ex. 24

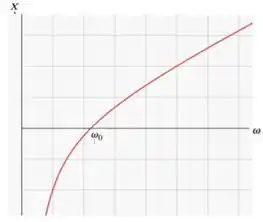
24. Defina a reatância de um circuito -- como . Mostre que quando a frequência angular é igual à frequência angular da ressonância . Qual é o sinal de para ? Qual é o sinal de para ? Faça um gráfico de contra

Passo 1

Essa questão vai pedir bastante a nossa interpretação de duas equações que conhecemos nesse capítulo.

Mas fique de boa, não é nada de outro mundo. Então vem que eu te mostro como é fácil.

Passo 2

Nesse item vamos usar a informação dada no enunciado que .

Então, para ,

Agora que achamos que é , vamos substituir em e ver o que acontece.

Prontinho, provado!

Passo 3

Sendo implicaria que seria um número maior que sendo assim ao subtrair os dois seria um número positivo.

Passo 4

Sendo implicaria que seria um número menor que sendo assim ao subtrair os dois seria um número negativo.

Passo 5

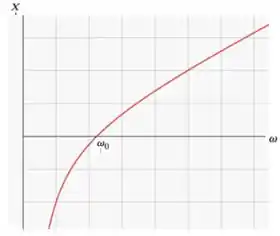
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23. Em um circuito R - L - C em série, a voltagem eficaz através do resistor é igual a 30,0V , através do capacitor é igual a 90,0V e através do indutor é igual a 50,0V . Qual é a voltagem eficaz da f

21. Análise de um circuito R - L - C . Você dispõe de um resistor de 200Ω , de um indutor de 0,400H , de um capacitor de 5,0μ F e uma fonte c a de frequência variável com amplitude de 3,0V . Todos ess

22. Um circuito R - L - C em série é construído com um resistor de 175Ω , um capacitor de 12,5μ F e um indutor de 8,0m H todos conectados através de uma fonte c a de frequência variável e uma amplitud

35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor