Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 121
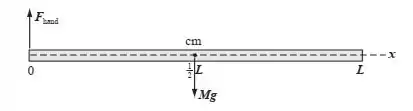
Uma demonstração comum em sala de aula consiste em tomar uma régua de madeira de um metro e segurá-la horizontalmente, pela extremidade de , com uma quantidade de moedas de um centavo igualmente espaçadas ao longo de sua superfície. Se a mão é, subitamente, relaxada, de modo que a régua começa a girar em torno da marca do zero sob a influência da gravidade, algo interessante é visto durante a primeira parte da rotação: os centavos mais próximas da marca do zero permanecem sobre a régua, enquanto os mais próximos da marca dos são abandonados pela régua. (Esta demonstração é muitas vezes referida como a demonstração do “mais rápido que a gravidade”.) Imagine esta demonstração repetida, sem nenhum moeda sobre a régua. (a) Qual seria, então, a aceleração inicial da marca dos ? (A aceleração inicial é a aceleração imediatamente após a largada.) (b) Qual ponto da régua teria, então, uma aceleração maior do que ?
Passo 1
- Bora lá, galerinha do bem! Nessa questão a gente vai analisar a rotação dessa régua, considerada como uma barra.
- A aceleração do ponto a uma distância do pivô vai ser:
Pela segunda lei de Newton para rotação:
Como é uma barra:
A gente relaciona a aceleração escalar com a angular pela formula .
Passo 2
Para a régua ter uma aceleração maior que a da gravidade:
Substituindo os valores numéricos: