Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 5.Problemas - Ex. 15
Demonstre a equação:
para
Passo 1
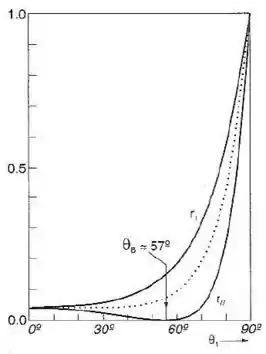
Para a questão, a demonstração pode ser explicada analisando o crescimento angular entre, no qual esse tem seu comportamento esboçado na figura abaixo.
Passo 2
Podemos observar que a curva de cima é referente a . Essa curva tem um perfil de crescimento exponencial.
Pelos conhecimentos de cálculo, sabemos que a derivada primeira de uma curva crescente em um ponto como é sempre maior que zero. Como a nossa curva cresce à medida que se aumenta , temos que:
Repare que o mesmo não acontece com a curva de , o qual apresenta um decréscimo devido ao ângulo de Brewster.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um feixe de luz não polarizada com uma intensidade de 10 mW / m 2 atravessa um filtro polarizador como na Fig. 33-11. Determine(a) a amplitude do campo elétrico da luz transmitida; (b) a pressão exerc
Na Fig. 33-41, um feixe luminoso com uma intensidade de 43W / m 2 e a polarização paralela ao eixo y atravessa um sistema composto por dois filtros polarizadores cujas direções fazem ângulos θ 1=70 °
Na Fig. 33-42, um feixe luz não polarizada passa por um conjunto de três filtros polarizadores. Os ângulos θ 1 ,θ 2 eθ 3 das direções de polarização são medidos no sentido ant horário no sentido posit
y positivo (os ângulos não estão desenhados em escala na figura). O ângulo θ 1 é fixo, mas o ângulo θ 2 pode ser ajustado. A Fig 33-45 mostra a intensidade da luz que atravessa o sistema em função de
Na Fig. 33-40, um feixe de luz inicialmente não polarizada atravessa três filtros polarizadores cujas direções de polarização fazem ângulos de θ 1 = 40 ° , θ 2= 20 ° , θ 3=40 ° com a direção do eixo y