Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.4 - Ex. 33
Na Fig. 33-40, um feixe de luz inicialmente não polarizada atravessa três filtros polarizadores cujas direções de polarização fazem ângulos de com a direção do eixo . Que porcentagem da intensidade inicial da luz é transmitida pelo conjunto?
(Sugestão: preste atenção nos ângulos.)
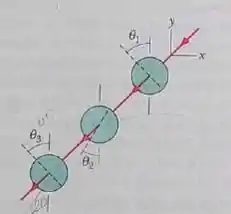
Passo 1
Como a luz é não polarizada, ao passar no primeiro filtro sua intensidade cai a metade:
Isso na direção de .
Passo 2
Agora quando passa pelo segundo filtro, o ângulo dele em relação ao eixo positivo é . Daí aqui usando a regra do cosseno para encontrar a intensidade :
E para o terceiro temos a mesma diferença entre ao ângulos, já que o terceiro filtro está na mesma posição que o filtro dois:
Passo 3
Assim a porcentagem é:
Resposta
Exercícios de Livros Relacionados
Faz-se girar um analisador de polarização em torno da direção da luz incidente como eixo, observando-se a intensidade da luz transmitida. (a) Mostre que isso não permite distinguir entre luz incidente
09. Use o operador D i v para obter a condição de contorno na interface entre dois meios quando existe sobre ela uma distribuição de carga com densidade superficial σ . Aplique o resultado a um condut
8. Chama-se eixo de um filtro de polarização (polarizador ou analisador) a direção de vibração para a qual sua transmissão é máxima. Um par de filtros têm seus eixos cruzados (perpendiculares), de mod
Seja 0 o ångulo entre os eixos de transmissão de duas placas polarizadoras. Luz não polarizada de intensidade I incide na primeira placa. Qual é a intensidade da luz transmitida através de ambas as pl
Desenhe um diagrama para explicar como os óculos de sol Polaróide reduzem o clarão da luz solar refletido em uma superfície horizontal plana, tal como a superficie de uma piscina. Seu diagrama deve in