Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 51

Os cavaleiros do rei Artur disparam um canhão do topo da muralha de um castelo. A bala de canhão é disparada com 50 m/s em um ângulo de 30º. Outra bala de canhão, que foi acidentalmente deixada cair, atinge o fosso do castelo abaixo em 1,5 s.

a. A que distância da muralha do castelo a bala de canhão atinge o solo?

b. Qual é a altura máxima atingida pela bala de canhão acima do solo?

Passo 1

Sabemos que

v 0 = 50   m / s

θ = 30 °

a y = - g

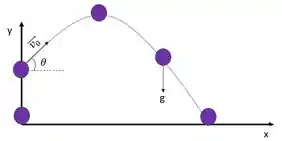
O movimento é composto em relação a x e a y, assim em relação a x é um Movimento Uniforme e em relação y é Movimento Uniformemente Variado.

O exercício pede para encontrar o x que é o nosso alcance em (a), e em (b) a altura máxima em relação a y.

Passo 2

  1. Encontrando a altura da muralha, considerando uma queda livre em que a velocidade inicial é zero da bala de canhão que caiu acidentalmente temos

    2. y = y 0 + v 0 y t - t 0 + g t - t 0 2 2 → 0 = y 0 + 0 - 9,8   .   1,5 2 2 → y 0 = 11,03   m

    Descoberto a altura da muralha, podemos ir para o movimento em si com a velocidade inicial de 50 m/s, para isso precisamos decompor em relação a x e a y.

    v 0 x = v 0 cos ⁡ 30 ° = 43,3   m / s

    v 0 y = v 0 sen ⁡ 30 ° = 25,5   m / s

    Agora substituindo na equação do movimento em relação a y para descobrir o tempo

    y = y 0 + v 0 y t - t 0 + a y t - t 0 2 2 → 0 = 11,03 + 25 t - 4,9 t 2

    Encontra-se t 1 = 5,51   s e t 2 = - 0,41   s , mas como t 2 é impossível fisicamente utilizamos   t 1 . Sabendo o tempo, agora definiremos o alcance da bala que é

    x = x 0 + v 0 x t - t 0 → 0 = 43,3   .   5,51 = 239   m

    O alcance foi de 239 m.

    Passo 3

  2. Para saber a altura máximo, temos que lembrar que a no topo a velocidade é zero, assim

v 2 = v 0 2 = 2 a y y - y 0 → 0 = 25 2 - 2   .   9,8   y - 11,03 → y = 42,9 m

A altura máxima é de 42,9 m

Resposta

  1. 239   m
  2. 42,9 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A rapidez de uma flecha ao abandonar o arco é de cerca de 45,0 m/s. (a) Um arqueiro, a cavalo, atira uma flecha a um ângulo de 10° acima da horizontal. Se a seta está 2,25 m acima do chão quando lança
Calculamos, no texto, o alcance de um projétil que cai no mesmo nível de onde foi lançado e encontramos R = v 0 2 g sin ⁡ 2 θ se a resistência do ar for ignorada. (a) Mostre que, sob as mesmas condiçõ
Um projétil é lançado a um ângulo θ acima do nível do chão. Um observador, parado no ponto de lançamento, vê o projétil em seu ponto de altura máxima e mede o ângulo ϕ mostrado na Figura 3-38. Mostre
Um canhão de brinquedo é colocado em uma rampa inclinada de um ângulo ϕ . Se a bala é projetada rampa acima a um ângulo θ 0 acima da horizontal, com uma rapidez inicial v 0 , mostre que o alcance R da
Uma mulher atira uma bola contra um muro vertical 4,0 m à sua frente. A bola está 2,0 m acima do chão quando abandona a mão da mulher com uma velocidade de 14 m/s a 45°, conforme mostrado. Quando a bo