Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.5 - Ex. 54
Demonstre a seguinte expressão para a intensidade luminosa da figura de difração produzida por uma “rede” de três fendas:
Onde e .
Passo 1
Vamos começar considerando a última informação que foi dada no enunciado: . Isso quer dizer que a largura das fendas é muito menor do que o comprimento de onda da luz que passa por elas.
Nesse caso, a envoltória de difração que seria produzida pela largura das fendas pode ser ignorada. Ou seja, podemos tratar esse problema como um de fendas infinitamente estreitas.
Beleza, então vamos escrever uma função para o campo elétrico que sai de uma das três fendas e chega até certo ponto na tela:
Ok, agora se outra onda sai de uma fenda logo acima dessa, separada por uma distância , qual vai ser a diferença de fase quando ela chega ao mesmo ponto da tela?
Ou seja, a segunda onda será:
E pela mesma lógica, a terceira será:
Passo 2
Agora vamos ver o que acontece quando esses três campos se combinam em algum ponto da tela. Para isso vamos usar um diagrama fasorial.
Para facilitar, começamos desenhando o diagrama com todos os fasores partindo da origem:
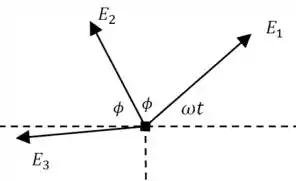
E agora desenhamos eles de forma que a soma fique mais fácil de entender (só vamos “transladar” alguns dos fasores):
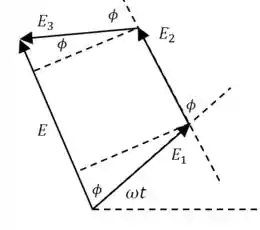
Lembrando que os fasores , e tem a mesma magnitude .
Passo 3
Agora é só usar um pouco de geometria plana para encontrar a magnitude do campo resultante :
Mas a intensidade é proporcional ao quadrado do campo elétrico, ou seja:
Onde é alguma constante de proporcionalidade, então:
Para determinar o valor da constante , só temos que perceber que o valor máximo da intensidade acontece quando , já que nesse caso o cosseno vale :
Beleza, agora é só substituir na nossa fórmula de cima:
Que é exatamente o que o enunciado pediu para demonstrarmos:
Resposta
Demonstração.