Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 1
Demonstre o seguinte teorema dos eixos perpendiculares: O momento de inércia de uma placa (lâmina delgada) plana de forma arbitraria em relação a um eixo perpendicular a seu plano, com a origem no plano da placa, é a soma dos momentos de inércia em relação aos eixos e , que formam com o um sistema de eixos ortogonais.
Passo 1
Como estamos tratando de uma lamina, podemos usar a densidade superficial, olhá só:
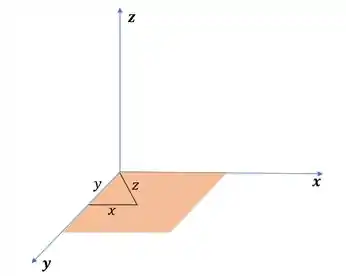
Passo 2
Com relação ao eixo , temos:
Como relação ao eixo é bem parecido!
Logo,
Isto é,
Passo 3
Agora vamos ver para o eixo .
Mas pelo terorema de Pitágoras, temos:
Logo
Portanto,
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Dois cilindros homogêneos, ambos girando em tomo do respectivo eixo central (longitudinal) com uma velocidade angular de 235r a d / s , têm a mesma massa de1,25k g e raios diferentes. Qual é a energia
A Fig. 10-33 mostra um arranjo de 15 discos iguais colados para formar uma barra de comprimento L=1 , 0000m e massa total M=100,0m g . O arranjo pode girar em tomo de um eixo perpendicular que passa p
Duas barras finas (ambas de massa 0,2 k g ) estão unidas para formar um corpo rígido como mostra a figura abaixo. Uma das barras tem comprimento L 1 = 0,4 m e a outra tem comprimento L 2 = 0,5 m . Qua
A barra fina e homogênea da Fig. 10-50 tem 2,0m de comprimento e pode girar, sem atrito, em torno de um pino horizontal que passa por uma das extremidades. A barra é liberada a partir do repouso e de
(a) Mostre que o momento de inércia de um cilindro maciço de massa M e raio R em relação ao eixo central é igual ao momento de inércia de um aro fino de massa M e raio R / 2 em relação ao eixo central