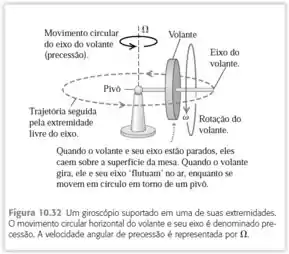
a) Desenhe uma vista de topo do giroscópio da Figura 10.32 indicando letras para , , e . Desenhe , produzido por . Desenhe +. Determine o sentido da precessão examinando as direções e sentidos de e +.

b) Inverta o sentido da velocidade angular do rotor e repita todas as etapas do item (a).

c) Mova o pivô para a outra extremidade do eixo, considerando a mesma direção e o mesmo sentido da velocidade angular de spin como na parte (b) e repita todas as etapas.

d) Mantendo o pivô como na parte (c), inverta a velocidade angular de spin do rotor e repita todas as etapas.

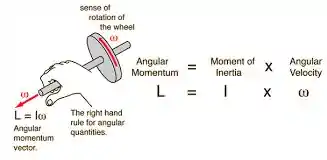
Quando o sistema de partículas for um corpo rígido girando em torno de um eixo de simetria, então e I é constante.

Quando esse eixo possui direção fixa no espaço, então os vetores e variam apenas em módulo, mas a direção e o sentido não variam. Assim,

A direção de é dada pela regra da mão direita, segundo a figura:

A representação do giroscópio esquematizado pela Figura 10.32 é

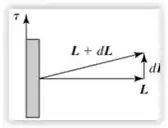
Tendo uma vista de topo, a precessão se da em sentido anti-horário, a velocidade angular também, e o comprimento , consequentemente, aponta para a direita.

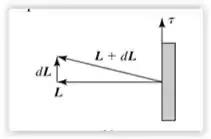
Invertendo o sentido da velocidade angular do rotor, a direção da precessão também inverte; o comprimento aponta para a esquerda, representando-se

Se movermos o pivô para a outra extremidade do eixo, considerando a mesma direção e o mesmo sentido da velocidade angular de spin, vamos ter o contrário da letra a

O torque altera o sentido, a velocidade de precessão é no sentido anti-horário.

Já quando mantemos o pivô como na parte (c), e invertendo a velocidade angular de spin do rotor, a representação é a seguinte

Fica igual a letra b, só que ao contrário também :D. A precessão é no sentido horário.