Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 48
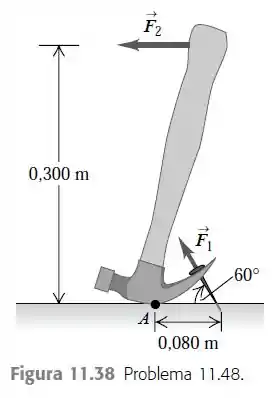
A garra de um martelo é usada para arrancar um prego de uma tábua (Figura ). O martelo faz um ângulo de com a tábua, e a força necessária para arrancar o prego possui módulo igual a . O contato entre a cabeça do martelo e a tábua ocorre no ponto A, situado a uma distância de do ponto onde o prego está cravado na madeira. Uma força horizontal é aplicada ao cabo do martelo a uma distância de acima da tábua. Qual é o módulo de força que deve ser aplicada para produzir a força de () necessária para arrancar o prego? (Despreze o peso do martelo.)
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular o módulo de força que deve ser aplicada no martelo para produzir a força de () necessária para arrancar o prego.
Para analisar essa situação, vamos considerar o martelo como um corpo livre e vamos considerar que ele está em equilíbrio, sendo assim a soma dos torques e das forças precisa ser zero.
Vamos ao Diagrama do Corpo Livre:
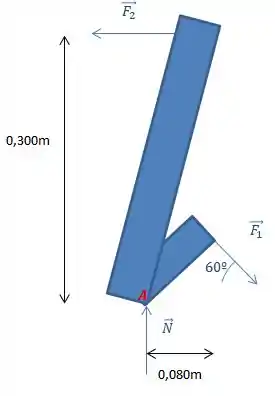
Se liga em duas coisas:
- A força que está no desenho do livro é a força que o prego sofre, a força no martelo é na direção contrária que é a força que o prego faz se opondo ao martelo que tenta tira-lo.
- Há uma força normal no ponto devido ao contato do martelo na tábua.
Como queremos calcular a força necessária e não queremos calcular a força normal que atua no ponto , faremos o somatório dos torques no ponto , pois assim não precisamos calcular a força normal que atua nesse ponto. Lembrando que,
Bora aplicar?
Passo 2
Fazendo o somatório dos torques no ponto e considerando o sentido anti-horário como positivo, teremos:
Se liga em duas coisas:
- O momento da força é negativo pois aponta no sentido horário, e é necessário multiplicar pelo seno de , para se obter a componente da força que é perpendicular ao braço de .
- Já o momento da força é positivo pois aponta no sentido anti-horário e não é necessário multiplicar pelo seno, pois a força já é perpendicular ao braço de .
Com isso ficamos com:
Colocando a força em evidência, teremos:
Logo, a força que deve ser aplicada ao cabo de martelo é muito menor que a força que o prego recebe do martelo, devido à grande diferença nos comprimentos dos braços do momento, o que mostra que o martelo funciona como uma alavanca.
Valeu, galera! Até a próxima! 😉