Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 29
Determine o campo magnético no eixo em se (a) ambas as correntes estão na direção e a corrente no fio em está na direção .
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
Certo! Vamos Denotar o fio (e corrente) a e o fio (e corrente) a . Podemos usar a equação para encontrar o campo magnético devido a cada um dos fios condutores de corrente e sobrepor os campos magnéticos devido às correntes nos fios para encontrar nos pontos dados no eixo .
Passo 2
Ainda sem entender? Vamos para os cálculos que vai facilitar a visualização. Observe a imagem abaixo:
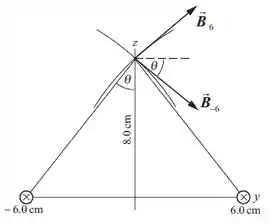
Certo! Vamos aplicar a regra da mão direita para mostrar que, para as correntes paralelas e na direção negativa, as direções dos campos são as mostradas acima.
Agora, Expressamos as magnitudes dos campos magnéticos em devido aos fios condutores de corrente em e :
Observando que os componentes acrescentam a zero, expressam o campo magnético resultante a :
Passo 3
Certo! Seguindo o mesmo estilo, aplicamos a regra da mão direita para mostrar que, para as correntes antiparalelas com a corrente no fio em na direção negativa, as direções dos campos são as mostradas abaixo:
Observando que os componentes acrescentam a zero, expressamos o campo magnético resultante em :
Passo 4
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.