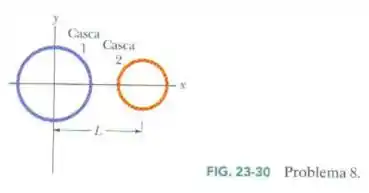
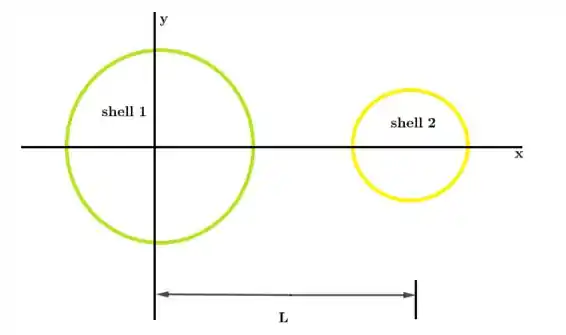
A Fig. 23-32 mostra duas cascas esféricas não condutoras mantidas fixas no lugar. A casca 1 possui uma densidade superficial de cargas uniforme de +6,0 μC/m2 na superfície externa e um raio de 3,0 cm; a casca 2 possui uma densidade superficial de cargas uniforme de +4,0 μC/m 2 na superfície externa e um raio de 2,0 cm; os centros das cascas estão separados por uma distância L = 10 cm. Em termos dos vetores unitários, qual é o campo elétrico no ponto x = 2,0 cm?

Primeiramente temos que perceber que esse ponto está dentro da casca esférica 1.

Temos que ficar atentos que o campo dentro de uma casca esférica devido a própria casca é zero. Isso irá acontecer pois toda a carga da casca esférica estará na sua superfície, e assim não haverá carga no interior da gaussiana e pela lei de gauss teremos que o campo é zero.

Ou seja, o campo elétrico nesse ponto será causado somente pela casca 2. A fórmula para o campo gerado por uma casca esférica é:

É importante se atentar a direção desse campo elétrico. O campo sai da carga positiva, dessa forma, o campo elétrico gerado pela casca 2 no ponto terá direção negativa.

Tendo em mãos a fórmula é só calcularmos a carga e depois o campo, com essas considerações que falamos aí, bora fazer isso?

Vamos começar calculando a carga total na casca esférica 2.

Usando a densidade superficial de cargas:

Substituindo a área da esfera temos:

Agora é substituir os valores, tanto do raio quando da densidade para a esfera 2.

Encontrada a carga vamos ao campo!

Lembrando que a distância entre a carga e a casca é . Podemos calcular o campo elétrico:

Substituindo a carga encontrada e temos: