Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 37

Determine as diferentes capacitâncias equivalentes que podem ser obtidas usando dois ou três dos seguintes capacitores: um capacitor de 1,00   μ F , um capacitor de 2,00   µ F e um capacitor de 4,00   µ F .

Passo 1

Primeiro... Vamos chamar C 1 = 1,00 μ F , C 2 = 2,00 μ F e C 3 = 4,00 μ F . Agora, antes de passar para o exercício em si, vamos ver quais são todos os tipos de arranjos com esses três capacitores.

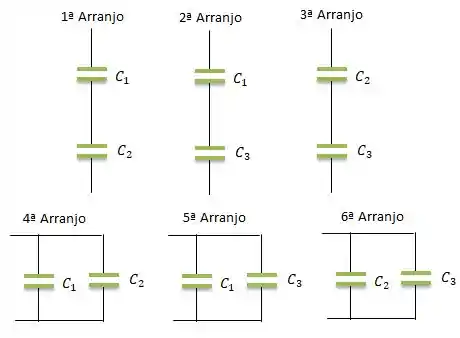
ARRANJOS COM DOIS CAPACITORES...

ARRANJOS COM TRÊS CAPACITORES...

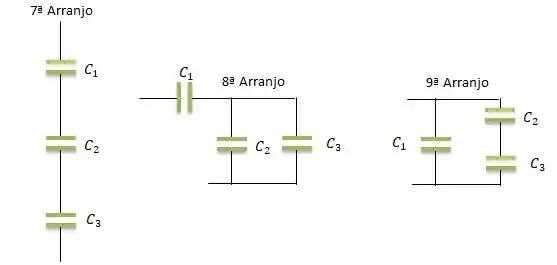
Repare que no arranjo de 3 Capacitores, poderíamos variar os outros capacitores, como trocar o C 2 por C 1 no 8 º e 9 º arranjos. Mas, aqui vamos fazer só esses, ta legal?

Passo 2

Primeiro vamos determinar as capacitâncias do primeiro grupo de arranjo...

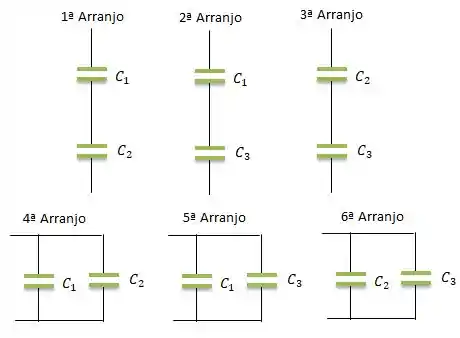
Para a primeira, segunda e terceiro arranjo...

C e q = C 1 C 2 C 1 + C 2 ;               C e q = C 1 C 3 C 1 + C 3 ;                     C e q = C 3 C 2 C 3 + C 2

Então, como C 1 = 1,00 μ F , C 2 = 2,00 μ F e C 3 = 4,00 μ F ...

C e q = 1 ⋅ 2 1 + 2 ;               C e q = 1 ⋅ 4 1 + 4 ;                     C e q = 2 ⋅ 4 4 + 2     →

C e q = 2 3 μ F ;               C e q = 4 5 μ F ;                     C e q = 8 6 = 4 3 μ F     →

Já para o 4 ª , 5 ª e 6 ª arranjos...

C e q = C 1 + C 2 ;             C e q = C 1 + C 3 ;             C e q = C 3 + C 2         →

C e q = 1 + 2 ;             C e q = 1 + 4 ;             C e q = 4 + 2         →

C e q = 3 μ F ;             C e q = 5 μ F ;             C e q = 6 μ F

Passo 3

Agora, olhando para o terceiro grupo de arranjos...

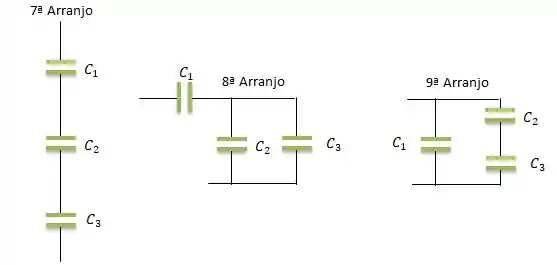
Para o 7 º arranjo, já vimos que essa associação em série gera...

C e q = C 1 C 2 C 3 C 1 C 2 + C 2 C 3 + C 1 C 3   →

C e q = 1 ⋅ 2 ⋅ 4 1 ⋅ 2 + 2 ⋅ 4 + 1 ⋅ 4   →

C e q = 8 2 + 8 + 4   →

C e q = 8 1 4 = 4 7 μ F

Para 8 ° arranjo...

C e q = C 1 C 2 + C 3 C 1 + C 2 + C 3       →

C e q = 1 2 + 4 1 + 2 + 4       →

C e q = 6 7 μ F  

E finalmente para o 9 ° arranjo...

C e q = C 1 + C 2 C 3 C 2 + C 3     →

C e q = 1 + 2 ⋅ 4 2 + 4     →

C e q = 1 + 8 6     →

C e q = 1 + 4 3 = 7 3 μ F

Resposta

1° Arranjo:

C e q = 2 3 μ F

2° Arranjo:

C e q = 4 5 μ F

3° Arranjo:

C e q = 4 3 μ F    

4° Arranjo:

C e q = 3 μ F

5° Arranjo:

C e q = 5 μ F

6° Arranjo:

C e q = 6 μ F

7° Arranjo:

C e q = 4 7 μ F

8° Arranjo:

C e q = 6 7 μ F

9° Arranjo:

C e q = 7 3 μ F

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16 . Para o sistema de capacitores mostrado na Figura E 24.16 , encontre a capacitância equivalente ( a ) entre b e c , e ( b ) entre a e c .
17 . Na Figura E 24.17 , cada capacitor possui C =4,00μ F e V a b = + 28,0V . Calcule ( a ) a carga de cada capacitor; ( b ) a diferença de potencial através de cada capacitor; ( c ) a diferença de po
19 . Na Figura 24.9 a , seja C 1 =3,00μ F , C 2 =5,00μ F e V a b = + 52,0V . Calcule ( a ) a carga em cada capacitor e( b ) a diferença de potencial através de cada capacitor.
63 . Uma diferença de potencial V a b = 48,0V é aplicada através do circuito de capacitores da Figura E 24.17 . Se C 1 = C 2 = 4,00μ F e C 4 = 8,00μ F , qual deve ser o valor da capacitância C 3 para
69 . Seu fornecedor de energia elétrica possui um conjunto de capacitores com capacitância C 1 e outro conjunto de capacitores com capacitância C 2 . Você terá que determinar os valores de C 1 e de C