Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 51
Ao tapear a superfície da água com sua cauda para anunciar perigo, um castor deve girá-la em torno de uma de suas extremidades estreitas. Modelemos a cauda como um retângulo de espessura e massa específica uniformes. Estime seu momento de inércia em relação à linha que passa por uma das extremidades estreitas (linha tracejada). Suponha a cauda medindo por , com uma espessura de , e que sua massa específica é igual à da água.
Passo 1
Oláaaaa, cê está bem?
Então, essa história toda do castor é basicamente o enunciado tentando dizer que ele quer o momento de inércia de uma placa retangular em relação ao eixo que passa por uma de suas arestas.
A gente não tem o momento de inércia de placas retangulares na nossa listinha do livro, né? Então vamos precisar usar integral para achar o momento de inércia.
Para fazer isso, a gente precisa montar essa integral:
Onde é a distância entre o eixo, em relação ao qual a gente quer o momento de inércia, e um elemento que pertence ao nosso sólido (a placa retangular).
Como assim “elemento”? Cara, é um pedacinho do nosso sólido. Aí esse pedacinho tem uma massa bem pequena , uma largura bem pequena , e tem a espessura da placa :
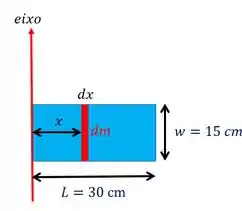
Percebe que a distância entre o eixo e o elemento é a mesma para todos os pontos de um elemento de largura e altura (o retângulo vermelho), por isso a gente pode usar esse retângulo fininho, que tem a mesma altura do retângulo como o nosso elemento
Agora bora ver como montar essa integral!
Passo 2
Vimos pela figura que vale para todos os pontos do elemento , então
Nossa integral fica
E pode ser escrito também em função de . Como? Vamos imaginar que a placa tem densidade , que é dada por
Onde é a massa da placa e o volume dela. Essa densidade é constante. Ela é a mesma para todos os pontos. Então a gente pode dizer que
Só que quem é é o volume do elemento. Como ele tem altura , espessura e largura , o volume é
Então fica:
Substituindo isso na integral:
Passo 3
Agora vamos calcular:
Falta só saber os nossos extremos de integração. Aí cê pode ver isso pela nossa figura. O menor valor que pode ter é e o maior é a largura do retângulo , então:
Nossa integral fica
Tira o que é constante de dentro da integral
Usa a regrinha de integrar polinômios:
Passo 4
Ele diz que a cauda (a placa retangular) tem a densidade da água. A densidade da água é (é bom gravar ela assim como a gente grava o valor da aceleração da gravidade).
Então agora é substituir os valores!
Para passar de para a gente vai multiplicar por , e para passar de para a gente vai multiplicar por , então vamos ter: