Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 121
Em um dia sem vento, um piloto faz uma demonstração com um antigo avião da Primeira Guerra, indo de Dubuque, Iowa, Para Chicago, Illinois. Desafortunadamente, ele não se dá conta de que a velha agulha magnética do aparelho está com um sério problema e o que ela registra como o “norte” é na realidade, 16,5° a leste do verdadeiro norte. Em dado momento de seu vôo, o aeroporto de Chicago notifica-o de que ele está 150 km a oeste do aeroporto. Ele aponta, então, para o leste, de acordo com a bússola do avião, e voa 45 minutos a 150 km/h, chegando ao ponto em que ele espera enxergar o aeroporto e começar a descida. Qual é a real distância até Chicago e qual deve ser agora a orientação do piloto para voar diretamente para Chicago?
Passo 1
Opa galera, vamos lá resolver esse problema. A grande sacada desse problema é interpretar as informações que nos foram dadas de forma clara. Pra isso trouxe essa figura para nos auxiliar.
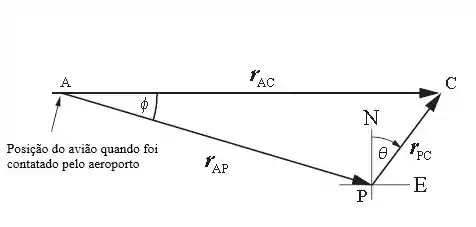
O problema diz que a bússola está com problemas e por isso ele voa com uma defasagem de a sul do leste como mostrado na figura. Então queremos a real distância entre o ponto em que o piloto vai estar que é o ponto P e o aeroporto de chicago que é o ponto C. Essa distância é dada por .
Para encontrarmos estas componentes precisamos saber o ângulo .
Passo 2
Como o problema trata de movimento relativo temos que:
O vetor pode ser descrito por:
Então:
O vetor é dado por:
Passo 3
Agora é só substituir os valores e correr pro abraço.