Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 122

Um avião de carga perdeu um pacote em vôo porque alguém esqueceu de fechar as portas traseiras do compartimento de carga. Você é membro da equipe de especialistas em segurança encarregada de analisar o que ocorreu. A partir da decolagem, ganhando altitude, o avião viajou em linha reta à rapidez constante de 275 mi/h a um ângulo de 37° acima da horizontal. Durante a subida, o pacote escorregou para fora da rampa traseira. Você encontrou o pacote em um campo a uma distância de 7,5 km do ponto da decolagem. Para completar a investigação, você precisa saber exatamente quanto tempo depois da decolagem o pacote abandonou a rampa. (Considere desprezível a rapidez de escorregamento na rampa.) Calcule quando o pacote caiu da rampa traseira. (Ignore a resistência do ar.)

Passo 1

Opa galera, vamos lá resolver esse problema. A primeira coisa a se fazer é tentar visualizar a situação e colocar no papel. Trouxe essa figura aqui que descreve o que aconteceu.

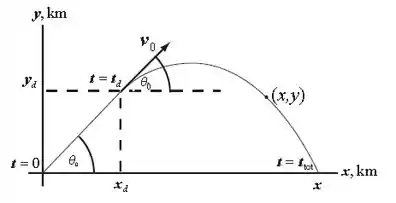
O problema diz que o avião estava decolando e em certo momento da decolagem a carga foi perdida. E o problema é justamente saber quando a carga foi perdida. Na figura esse tempo é representado por t d , então esta é a informação que queremos.

Bom, analisando a figura fica mais fácil de interpretar a situação toda. O avião faz a decolagem em linha reta com uma angulação de 37 ° acima da horizontal e no momento t d o pacote é perdido. O pacote então fica sujeito a um movimento parabólico como descrito na figura até o chão. Este ponto no chão está a 75   k m de distância do ponto de decolagem.

Com essas informações podemos traçar uma estratégia. Vamos expressar as coordenadas em x e y para o ponto de caída.

x d = v x , d   ⋅ t d

y d = v y , d   ⋅ t d

Para o movimento parabólico temos que:

x ( t ) = x d + v x , d ( t - t d )

y t = y d + v y , d t - t d - 1 2 g t - t d 2

Podemos então organizar as equações da seguinte forma:

x ( t ) = v x , d   ⋅ t d + v x , d ( t - t d )

y t = v y , d   ⋅ t d + v y , d t - t d - 1 2 g t - t d 2

y t = v y , d   ⋅ t - 1 2 g t - t d 2

Passo 2

Agora que já temos nossas equações dos movimentos vamos organizar nossas variáveis. Temos que:

v x , d   = v 0 ⋅ cos ⁡ θ 0

v y , d   = v 0 ⋅ sin ⁡ θ 0

Bom agora vamos substituir nosso valores. Mas antes temos que expressar nossa velocidade em m/s.

v 0 = 275 m i h ⋅ 1609 m m i ⋅ 1   h 3600   s

v 0 = 122,91   m / s

Então:

v x , d   = 98,16   m / s

v y , d   = 73,97   m / s

Passo 3

Analisando nossas condições temos que x t t o t = x l e y t t o t = 0 . Agora é só substituir os valores e correr pro abraço.

t t o t = x l v x , d

0 = v y , d   ⋅ t t o t - 1 2 g t t o t - t d 2

0 = v y , d   ⋅ x l v x , d - 1 2 g x l v x , d - t d 2

Resolvendo, temos que:

t d 2 - 2 x l v x , d   t d + x l 2 v x , d 2 - 2 x l ⋅ v y , d   g ⋅ v x , d   = 0

t d 2 - 2 ⋅ 7,5 98,16 t d + 7,5 2 98,16 2 - 2 ⋅ 7,5 ⋅ 73,97 9,81 ⋅ 98,16 = 0

t d 2 - 152,8 ⋅ t d + 4686 = 0

Resolvendo a equação encontramos t d = 110 s   o u   42 s . Como 110s nos confere uma distância muito longa:

t d = 42   s

Resposta

t d = 42   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois grilos, Chirpy e Milada, saltam do topo de um rochedo íngreme. Chirpy simplesmente se deixa cair e chega ao solo em 3.50 s, enquanto Milada salta horizontalmente com velocidadeinicial de 95,0 cm/
Um helicóptero militar em missão de treinamento voa horizontalmente com velocidade de 60,0m / s e acidentalmente deixa cair uma bomba (felizmente não ativa) de uma altura de 300 m . Despreze a resistê
Uma ousada nadadora salta correndo 510 N e horizontalmente de um rochedo para ummergulho, conforme a Figura 3.39. Qual deve ser sua velocidade mínima quando salta do topo do rochedo, de modo que ela c
Uma bola de gude rola horizontalmente com velocidade escalar v 0 e cai do topo de umaplataforma de 2,75m de altura, sem sofrer nenhuma resistência significativa do ar.No nível do solo, a 2,0m da base
Durante uma tempestade, um carro chega onde deveria haver uma ponte, mas o motorista a encontra destruída, levada pelas águas. Como precisa chegar ao outro lado, o motorista decide tentar saltar sobre