Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 2.Problemas Adicionais - Ex. 104
Um próton se move ao longo do eixo x de acordo com a equação , em que x está em metros e t está em segundos. Calcule (a) a velocidade do próton durante os primeiros do percurso, (b) a velocidade instantânea do próton no instante t = 3,0 s e (c) a aceleração instantânea do próton no instante . (d) Plote o gráfico de x em função de t e mostre como a resposta do item (a) pode ser obtida a partir do gráfico. (e) Indique a resposta do item (b) no gráfico. (f) Plote o gráfico de em função de e indique a resposta do item (c).
Passo 1
Para calcularmos a velocidade do próton para um dado tempo, precisaremos derivar a equação do movimento que foi dada no enunciado para obtermos a velocidade instantânea:
Na letra (a), o enunciado nos pede para encontrarmos a velocidade de 0 s até 3,0 s, então vamos calcular a diferença das velocidades para esses dois instantes:
Passo 2
(b) No instante , a velocidade do próton será:
Passo 3
(c) A aceleração instantânea do próton será a segunda derivada da equação de movimento, ou a primeira derivada da equação de velocidade:
Como a equação não depende do tempo, a aceleração instantânea para qualquer tempo t será:
E então para :
O que responde a letra (c).
Passo 4
(d) e (e) A resposta dos itens (a) e (b) pode ser obtida a partir do seguinte gráfico:
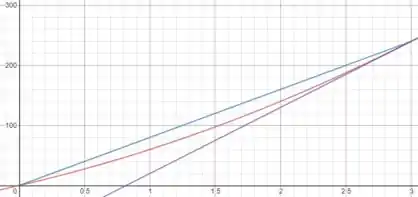
Onde a linha azul representa a resposta do item (a) que é a reta com coeficiente igual ao valor da velocidade média entre os instantes e , e a reta roxa a resposta do item (b), que é a reta tangente à curva para
Passo 5
(f) A resposta do item (c) no seguinte gráfico:
Será a curva da velocidade, e a aceleração instantânea para coincide com a reta de velocidade.