Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 46
Um módulo de aterrissagem lunar, de , encontra-se em órbita acima da superfície da Lua. Ele deve passar para uma órbita de de altitude a fim de se conectar à nave-mãe, que levará os astronautas para casa. Qual é a quantidade de trabalho que os propulsores precisarão realizar?
Passo 1
Se liga na figura!
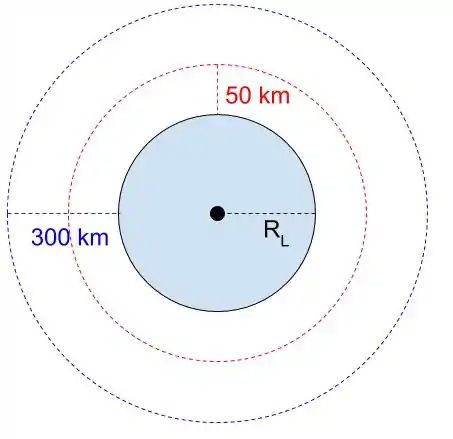
Repare que na órbita vermelha a distância do módulo de aterrisagem é
já na órbita azul
Passo 2
Podemos escrever que a energia potencial no início é igual
E no final é
Passo 3
O trabalho será a variação da energia entre as órbitas.
Sendo a constante gravitacional, o raio e a massa da lua iguais a
respectivamente, e que a massa do módulo de aterrisagem é
Podemos substituir os valores na equação (1) para achar o trabalho
Resposta
Exercícios de Livros Relacionados
Quanta energia um ônibus espacial de 50.000 kg deve perder para se transferir de uma órbita circular de 500 km de altura a uma órbita mais baixa de 300 km de altura?Dê uma descrição qualitativa da sit
A Figura 13.18 mostrou um gráfico de l o gT versus l o gr para os dados planetários da Tabela 13.2. Este tipo de gráfico é chamado de gráfico l o g - l o g . As escalas da Figura 13.18 são logarítmica
A FIGURA P13.54 mostra dois planetas de massa m orbitando uma estrela de massa M . Os planetas estão na mesma órbita, de raio r , mas estão sempre nas extremidades opostas de um diâmetro. Obtenha uma
As duas estrelas de um sistema estelar binário têm massas de 2,0 × 10 30 kg e 6,0 × 10 30 kg. Elas estão separadas por 2,0 × 10 12 m de distância. Qual é: a. O período de rotação do sistema, em anos?
Três estrelas, cada uma com a massa do Sol, formam um triângulo equilátero com lados de 1,0 × 10 12m . (Este triângulo se encaixaria com precisão na órbita de Júpiter). O triângulo precisa girar, pois