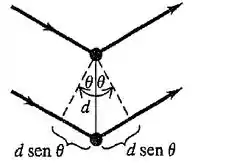
A Difração de elétrons pode ocorrer também quando existe interferência entre as ondas dos elétrons espalhados pelos átomos sobre a superfície do cristal e as ondas dos elétrons espalhados pelos átomos da camada imediatamente abaixo da superfície do cristal, situados a uma distância abaixo da superfície (veja a Figura 36.23c). (a) Elabore uma equação para o ângulo referente a um máximo da figura de difração no caso de elétrons de comprimento . (b) O espaçamento entre os planos do cristal de um metal é igual a 0,091 nm. Usando elétrons de 71,0 eV, calcule o ângulo em que ocorre um máximo produzido pela interferência entre as ondas espalhadas de planos adjacentes do cristal. O ângulo é medido como na Figura 36.23c. (c) O ângulo real referente à intensidade máxima é ligeiramente diferente daquele que você calculou no item (b). A explicação é que a função trabalho do metal (veja a Seção 38.2) faz a energia potencial do elétron mudar de quando ele sai do vácuo e penetra no metal. Quando consideramos o feito da função trabalho o ângulo referente à intensidade máxima é maior ou menor do que o ângulo calculado no item (b) ? Explique.

letra b)

Precisamos agora calcular o ângulo em que ocorre o máximo de interferência.

Como no enunciado não temos o comprimento de onda, iremos calcular a partir da energia.

Se usarmos a relação de De Broglie, podemos relacionar o comprimento de onda com o momento linear.

E como podemos escrever a energia como sendo , o comprimento então será:

Então teremos que:

Para o máximo , então:

letra c)

A função trabalho do metal atua como um potencial atrativo, aumentando a energia cinética dos elétrons que estão entrando em . Um aumento na energia cinética é um aumento no momento que leva a um comprimento de onda menor. Um comprimento de onda menor fornece um ângulo menor