Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.4 - Ex. 7
As dimensões de uma sala são (altura) X X . Uma mosca parte de um canto da sala e pousa em um canto diagonalmente oposto. (a) Qual é o módulo do deslocamento da mosca? (b) A distância percorrida pode ser menor que este valor? (c) Pode ser maior? (d) Pode ser igual? (e) Escolha um sistema de coordenadas apropriado e expresse as componentes do vetor deslocamento em termos de vetores unitários. (f) Se a mosca caminhar, em vez de voar, qual é o comprimento do caminho mais curto para o outro canto? (Sugestão: o problema pode ser resolvido sem fazer cálculos complicados. A sala é como uma caixa; desdobre as paredes para representá-las em um mesmo plano antes de procurar uma solução.)
Passo 1
Este é um problema que envolve a visualização do espaço tridimensional e, por isso, trabalha a noção vetorial.
Para entendermos melhor o que está se passando, vamos fazer uma ilustração representando a caixa e o deslocamento da mosca.
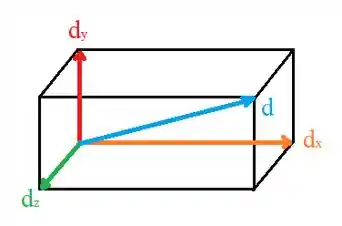
Nesta ilustração, o deslocamento da mosca é representado pela letra , enquanto isso, podemos visualizar os lados da caixa, que pode ser considerada como sendo as componentes de um vetor .
Portanto, para resolver este problema, usaremos a definição de módulo de vetor:
Passo 2
Para determinar o deslocamento da mosca, podemos visualizar, como explicitado no passo anterior, os lados da caixa como as componentes do vetor deslocamento diagonal de ponto a ponto. Assim, utilizando a definição de módulo de vetor:
Passo 3
Como a menor distância entre dois pontos é uma reta e, entre as duas quinas, a reta é a diagonal, então a mosca percorreu o menor caminho. Por isso, a distância percorrida pela mosca só pode ser maior ou igual, nunca menor.
Passo 4
Aproveitando a ilustração feita no passo inicial, vamos estabelecer o eixo de coordenada seguindo as arestas da caixa, de forma que:
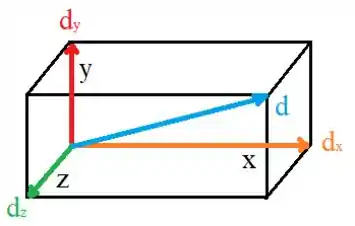
Portanto, o nosso vetor deslocamento pode ser escrito em função dos lados da caixa:
Passo 5
Para determinar o menor caminho que a mosca faria andando para o mesmo deslocamento, o pulo do gato é deitar a parede no chão para encontrar a reta entre os dois pontos.
Essa ficou um pouco abstrata, né? Para melhorar a visualização, dá uma olhadinha na ilustração abaixo e pense numa visão superior, ok?
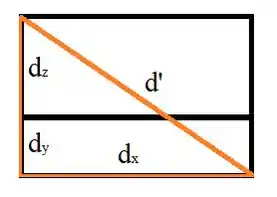
Então, para determinar essa distância, usamos Pitágoras:
Resposta
- ;
- ;
- ;
- ;