Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 100
Um carro que se move com aceleração constante percorreu em a distância de que separa dois pontos. A velocidade do carro ao passar pelo segundo ponto era . (a) Qual era a velocidade no primeiro ponto? (b) Qual era o módulo de aceleração? (c) A que distância do primeiro ponto o carro se encontrava em repouso? (d) Desenhe os gráficos de em função de e em função de para o carro, desde o repouso até o segundo ponto.
Passo 1
Este é um problema de MRUV, ou seja, movimento com aceleração constante. Para iniciar este exercício, como ele quer a velocidade do carro no primeiro ponto, vamos usar as duas fórmulas de velocidade que nós temos de MRUV:
Considerando o instante inicial como sendo o instante em que o carro passa pelo primeiro ponto e o instante final como sendo o instante em que o carro passa pelo segundo ponto, e sabendo que o enunciado nos deu a informação da velocidade no segundo ponto , com e o , podemos reescrever as fórmulas acima substituindo os valores:
Colocando na a aceleração em função da velocidade inicial , temos:
Substituindo a aceleração encontrada acima na , temos:
Colocando tudo para um lado só:
Resolvendo a equação do 2º grau aplicando Bhaskara, encontramos as seguintes raízes:
Como a velocidade no ponto inicial é necessariamente menor do que no ponto , então:
Passo 2
Para calcular a aceleração do carro, podemos usar diretamente a encontrada no passo anterior, substituindo o valor encontrado também no item anterior:
Passo 3
Para encontrar a distância do primeiro ponto que o carro se encontrava em repouso usaremos a famosa equação de Torricelli:
Onde consideraremos o ponto inicial como sendo o ponto em que o carro se encontra em repouso e o ponto final como sendo o primeiro ponto. Além disso, teremos que usar o valor da aceleração calculada no item anterior, assim:
Isolando o , temos:
Portanto, a distância do primeiro ponto que o carro se encontrava quando em repouso é .
Passo 4
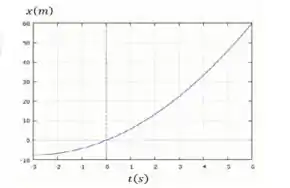
Para desenhar os gráficos temos que lembrar que este é um MRUV, logo, a função do deslocamento é uma função do segundo grau, enquanto o da velocidade é uma função do primeiro grau. Caso fossemos desenhar o gráfico da aceleração, este seria uma função constante.
Pois bem, vou anexar aqui um rascunho dos gráficos para completar a questão, mas o mais importante é você se lembrar da cara das funções, certo?
Resposta
- ;
- ;
- .