O objetivo de um navio échegar a um porto situado 120k m ao norte do ponto de partida, mas uma tempestade inesperada o leva para um local situado 100k m a leste do ponto de partida. (a) Que distância o navio deve percorrer e (b) qual o rumo deve tomar para chegar ao destino?

d = 156,2k m ; θ = 50,2 ° de oeste para norte.

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.4 - Ex. 5

O objetivo de um navio échegar a um porto situado ao norte do ponto de partida, mas uma tempestade inesperada o leva para um local situado a leste do ponto de partida. (a) Que distância o navio deve percorrer e (b) qual o rumo deve tomar para chegar ao destino?

Passo 1

Para entendermos essa questão vamos iniciar fazendo uma ilustração:

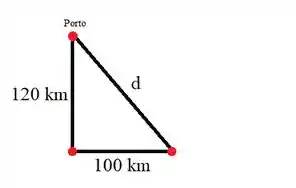
O navio deseja chegar no porto a ao norte de onde o navio parte, porém devido a tempestade ele se desloca para o leste. Para resolvermos a distância que ele precisa percorrer para chegar no porto, podemos aplicar o teorema de Pitágoras, pois podemos imaginar um triângulo retângulo ligando os pontos, como mostra a ilustração acima, então:

Passo 2

Para determinar o rumo que o navio deve tomar para alcançar o porto podemos determinar um ângulo o triângulo retângulo que ilustramos acima.

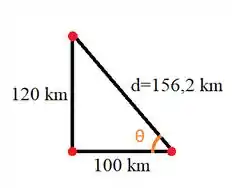Então, usando a definição de cosseno:

Logo,

Portanto, o navio deve se deslocar num grau de de oeste para norte.

Resposta

;
de oeste para norte.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro viaja 50k m para leste, 30k m para o norte e 25k m em uma direção 30 ° a leste do norte. Desenhe o diagrama vetorial e determine (a) o módulo e (b) o ângulo do deslocamento do carro em relaçã

(a)Determine a soma a → + b → , em termos de vetores unitários, para a → = 4,0m i ^ + ( 3,0m ) j ^ e b ^ = 13,0m i ^ + ( 7,0m ) j ^ . Determine (b) o módulo e (c) a orientação de a → + b → .

Três vetores, a → , b → e c → , têm o mesmo módulo, 50m , e estão em um plano x y . Os ângulos dos vetores em relação ao semieixo x positivo são 30 ° , 195 ° , e 315 ° , respectivamente. Determine (c)

Dois vetores são dados por a → = 4,0m i ^ - 3,0m j ̂ +1,0m k ^ e b → = - 1,0m i ^ +1,0m j ^ + 4,0m k̂ . Determine, em termos de vetores unitários, (a) a → +b⃗ ; (b) a → -b⃗ ; (c) um terceiro vetor, c⃗

Você deve executar quatro deslocamentos sucessivos na superfície plana num deserto, começando na origem de um sistema de coordenadas x y e terminando nas coordenadas ( - 140m ,30m ) . As componentes d