Uma boladeira é composta por três esferas pesadas iguais, ligadas a um ponto comum por cordas resistentes de mesmo comprimento (figura a). Para lançar esta arma inventada na América do Sul você segura uma das esferas acima da cabeça e faz a mão girar em torno do pulso para fazer as outras duas esferas girarem em um plano horizontal em torno da mão. Depois de conseguir uma velocidade de rotação suficiente você arremessa a arma em direção ao alvo. Inicialmente a boladeira gira em torno na esfera que foi mantida fixa, mas em pouco tempo todas as esferas passam a girar em torno do ponto comum das três cordas com velocidade anglar , (figura ). (a) Qual é a razão ? (b) Qual é a razão das energia cinéticas de rotação correspondentes no referencial do centro de massa?
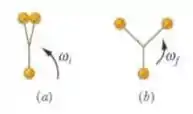
Passo 1
Depois que você solta o conjunto de esferas, o momento angular delas permanece constante, certo? Então podemos escrever os seguinte:
Beleza, então para calcular a razão entre as velocidades angulares, só precismos escolher algum eixo conveniente, e então ver o que acontece com o momento de inércia do sistema em relação a esse eixo.
Passo 2
Vamos fazer um desenho para calcular o momento de inércia. No primeiro caso, vamos supôr que as duas bolas de cima estão praticamente “uma em cima da outra”.
As duas bolas que não estão fixas vão girar em torno da bola de baixo, então:
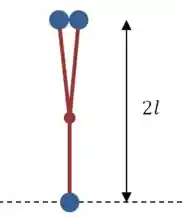
Onde estamos calculando o momento em relação ao eixo que é perpendicular ao plano da página, e passa pela bola de baixo.
Então o momento de inércia é:
Passo 3
E no segundo caso a rotação é em, torno do ponto central. Dessa vez a distância até o eixo é a mesma para todas as bolas:
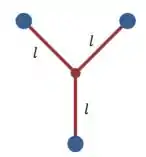
Passo 4
(a) Agora podemos calcular a razão entre as velocidade angulares:
Passo 5
(a) Agora vamos calcular a razão das energia cinéticas de rotação, lembrando que a fórmula dessa energia é:
Então a razão é:
O primeiro parênteses na esquerda é o inverso da razão que nós acabamos de calcular, e o segundo é a mesma razão.
Resposta
(a) A razão entre a velocidade angulares é .
(b) A razão entre as energia cinéticas de rotação é .