Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 55
O disco na Figura 10.25 tem massa de . A distância dele do centro de rotação é originalmente , e ele está deslizando com uma velocidade de . O fio é puxado para baixo a através do orifício na mesa sem atrito. Determine o trabalho realizado sobre o disco.
(Sugestão: Considere a mudança da energia cinética.)
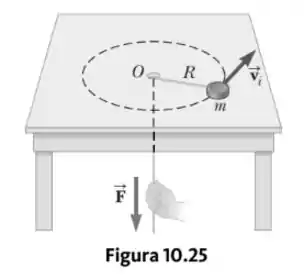
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Para avaliar a mudança na energia cinética do disco, nós primeiro vamos calcular os momentos de inércia inicial e final do disco:
Passo 2
A velocidade angular inicial do disco é dada por:
Agora, use a conservação do momento angular para o sistema do disco:
O trabalho é
Substituindo os valores temos:
Resposta
Exercícios de Livros Relacionados
Uma plataforma horizontal com a forma de um disco circular gira sem atrito em torno de um eixo vertical que passa pelo centro do disco. A plataforma tem uma massa de 150k g , um raio de 2,0m e um mome
Uma bailarina começa um tour jeté (Fig. 11-19a) com uma velocidade angular ω i e um momento angular formado por duas partes: I p e r n a = 1,44k g ∙ m 2 da perna estendida, que faz um ângulo θ = 90,0
A Fig. 11-52 é uma vista de cima de uma barra fina homogênea, de comprimento 0,800m e massa M , girando horizontalmente a 20,0r a d / s , no sentido anti-horário, em torno de um eixo que passa pelo ce
Uma mesa giratória grande, com raio de 6,00 m, gira em torno de um eixo vertical fixo, fazendo uma volta em 8,00 s. O momento de inércia da mesa em torno de seu eixo é de 1.200 kg m2 . Você para, desc
Você pendura um aro fino de raio R em um prego na periferia do aro. Você o desloca lateralmente até um ângulo β a partir de sua posição de equilíbrio e a seguir o liberta. Qual é sua velocidade angula