Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 8

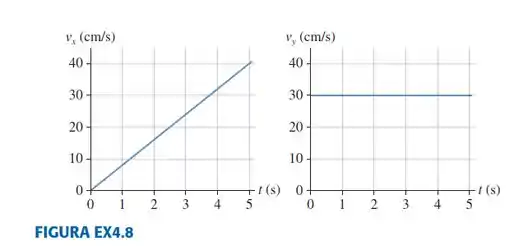
8 . || Um disco de hóquei movido a foguete move-se sobre uma mesa horizontal sem atrito. A F I G U R A   E X 4.8 mostra os gráficos de v x e de v y , os componentes x e y da velocidade do disco. Ele parte da origem.

a . Com que orientação o disco está se movendo em t   =   2   s ? Dê sua resposta na forma de um ângulo com o eixo x .

b . A que distância da origem se encontra o disco em   t   =   5   s ?

Passo 1

a . Com que orientação o disco está se movendo em t   =   2   s ? Dê sua resposta na forma de um ângulo com o eixo x .

Vamos aplicar a relação trigonométrica da representação vetorial e polar, veja:

v e t o r i a l : a i ^ + b j ^    

p o l a r : r ∠ θ

Nós temos que achar esse θ :

θ =   tan - 1 ⁡ b a

No nosso caso o a = v x e b = v y :

θ =   tan - 1 ⁡ v y v x

Pelos gráficos v y = 30 c m / s e v x ≅ 16 c m / s :

θ =   tan - 1 ⁡ 30 16

θ = 62 °   a n t i - h o r a r i o   a   x

Passo 2

b . A que distância da origem se encontra o disco em   t   =   5   s ?

Lembre-se que a posição é a integral da velocidade.

Ou melhor ainda... a variação de posição é a integral da velocidade com limites de integração sendo os t’s (tempo) dessas variações.

Mas também sabemos que a integral é equivalente a área de uma função.

Se estiver confuso com o texto acompanhe as fórmulas e os comentários, que vai ficar melhor:

Para x :

x 1 - x 0 ⏞ v a r i a ç ã o   d e   p o s i ç ã o =   ∫ 0 5 s v x d t ⏞ i n t e g r a l   d a   v e l o c i d a d e   =   á r e a !  

x 1 - 0     = 40 ⋅ 5 2

x 1     = 100 c m

Para y:

y 1 - y 0 ⏞ v a r i a ç ã o   d e   p o s i ç ã o =   ∫ 0 5 s v y d t ⏞ i n t e g r a l   d a   v e l o c i d a d e   =   á r e a !

y 1 - 0     = 30 ⋅ 5

y 1   = 150 c m

Mas veja que chegamos a uma reposta decomposta em x e y , então precisamos achar uma resultante, ou em outras palavras achar o módulo, ou ainda em outras palavras achar o “ r ” de uma representação polar.

Fazemos:

s 1 = 100 i ^ + 150 j ^

s 1 = r 1 = x 1 2 + y 1 2  

s 1 = r 1 = 100 2 + 150 2  

s 1 = r 1 = 180 c m

E essa é a resposta de forma aplicada.

Resposta

a

62 ° ,   a n t i - h o r á r i o   a   + x

( b )

180 c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula inicialmente localizada na origem tem aceleração de a →=3,00j ^m / s 2 e velocidade inicial de v i →=5,00i ^m / s . Encontre (a) o vetor posição da partícula em qualquer momento t , (b)
A velocidade do projétil quando atinge sua altura máxima é a metade de sua velocidade na metade da sua altura máxima. Qual é o ângulo de projeção inicial do projétil?
Em t=0 , uma partícula que se move no plano x y com aceleração constante tem uma velocidade de v i →=( 3,00i ^–2,00j ^ )m / s e está na origem. Em t=3,00s , a velocidade da partícula é v f →=( 9,00i ^
Um peixe nadando em um plano horizontal tem v e l o c i d a d e i=( 4,00i ^+1,00j ^ )m / s em um ponto do oceano onde a posição relativa a uma determinada pedra é r i →( t )=( 10,0i ^–4,00j ^ )m . Apó
O pequeno peixe arqueiro (comprimento de 20c m a 25c m ) vive em águas salobras do sudeste da Ásia, entre Índia e Filipinas. Essa criatura, cujo nome é apropriado, captura sua presa atirando um jato d