|| Um veleiro está viajando para leste a Uma forte rajada de vento imprime ao barco uma aceleração . Qual será a rapidez do barco e sua orientação mais tarde, quando a rajada some?
Passo 1
Um esquema é:
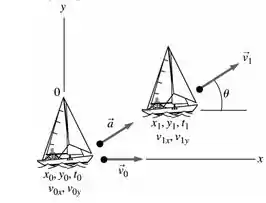
Antes de começar a fazer saiba que o termo rapidez é equivalente a velocidade, as vezes confundimos com aceleração. Por isso tome cuidado.
O que precisamos para essa questão é relacionar aceleração e velocidade, para poder achar esse último.
Precisamos de alguns conhecimentos de vetores e de trigonometria. A ideia é simples... decompor vetores para forma retangular e e ir aplicando as fórmulas.
Passo 2
Vamos decompor a aceleração em termos dos componentes e.Lembre-se de decomposição vetoriais e de trigonometria.
A aceleração nesse caso vai ser decomposta em:
Componente
Componente
Dessa forma o resultante fica:
Passo 3
Sabemos que uma das equações da velocidade é:
Então vamos desenvolver isso com os dados que temos, para achar .
Passo 4
Agora que temos , vamos representa-lo como um único número, ou em outras palavras, vamos achar o seu módulo.
Passo 5
Falta o ângulo, para ficar completo, mas uma vez usando trigonometria podemos usar a função , para achar o ângulo. Lembrando que tangente é seno sob cosseno, ou cateto oposto sob cateto adjacente.
, na região nordeste
Pronto.
Resposta
, na região nordeste