Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 56

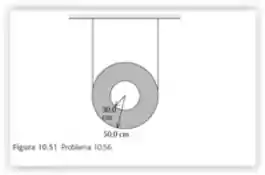
Um disco oco uniforme possui dois pedaços de cabo leve e fino em torno da sua borda externa e está suspenso do teto (Figura 10.51). De repente um dos cabos se rompe, e o cabo restante

não desliza enquanto o disco rola para baixo. Use a lei da conservação da energia para achar a velocidade escalar do centro desse disco, após ele ter caído por uma distância de 1,20 m.

Passo 1

A energia cinética para o disco é dada por

K = 1 2 M v c m 2 + 1 2 I ω 2

No momento em que o cabo se rompe, a energia potencial gravitacional diminui e a energia cinética aumenta. Por isso, representamos por:

K 1 + U 1 = K 2 + U 2

Então, inicialmente K 1 = 0 e U 1 = 0 . Lembrando que ω = v c m R .

Passo 2

Para R1=0,300 m e R2=0,500 m.

Assim, temos

0 + 0 = K 2 + U 2

0 = 1 2 M v c m 2 + 1 2 I ω 2 + M g y 2

Mas e a altura y2?? Bom, sabemos que y1=0, mas y2=-1,20m, negativo, pois o disco se desloca para baixo.

Substituindo,

0 = 1 2 M v c m 2 + 1 2 I ω 2 + M g y 2

- M g y 2 = 1 2 M v c m 2 + 1 2 I c m ω 2

Sendo I c m = 1 2 M ( R 2 + R 1 ) 2 , vamos organizar...

1 2 I c m ω 2 = 1 4 M [ 1 + R 1 R 2 2 ] v c m 2

1 2 I c m ω 2 = 1 4 M [ 1 + 0,3 0,5 2 ] v c m 2

1 2 I c m ω 2 = 0,34 M v c m 2

Voltando na equação - M g y 2 = 1 2 M v c m 2 + 1 2 I c m ω 2 ,

- M g y 2 = 1 2 M v c m 2 + 0,3 4 M v c m 2

- M g y 2 = 0,84   M v c m 2

Corta-se os termos semelhantes (M),

v c m 2 = - g y 2 0,84

v c m = ( - 9,8 m s 2 ) ( - 1,2   m ) 0,84

v c m = 3,74   m / s

Resposta

Resposta: v c m = 3,74   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma roda de 32,0 kg, essencialmente um aro fino com 1,20 m de raio, está girando a 280 rev/min. A roda precisa ser parada em 15,0 s. (a) Qual é o trabalho necessário para fazê-la parar? (b) Qual é a p
Na Figura abaixo, três partículas de 0,0100 kg foram coladas em uma barra, de comprimento L = 6,00 cm e massa desprezível, que pode girar em torno de um eixo perpendicular que passa pelo ponto O em um
Na Figura abaixo, três partículas de 0,0100 kg foram coladas em uma barra, de comprimento L = 6,00 cm e massa desprezível, que pode girar em torno de um eixo perpendicular que passa pelo ponto O em um
Uma casca esférica homogênea de massa M = 4,5 kg e raio R = 8,5 cm pode girar em torno de um eixo vertical sem atrito (Fig. 10-44). Uma corda de massa desprezível está enrolada no equador da casca, pa
Uma barata de massa 0,17 k g corre no sentido anti-horário na boda de um disco circular de raio 15 c m e momento de inércia 5.10 - 3 k g . m ² ², montado em um eixo vertical com atrito desprezível. A