Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 53
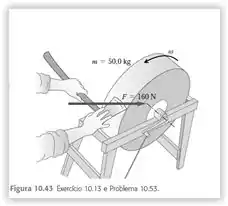
Um esmeril de é um disco sólido de diâmetro igual a . Você comprime um machado sobre a periferia com uma força normal de (Figura 10.43). O coeficiente de atrito cinético entre a lâmina e a pedra do esmeril é igual a , e existe um torque do atrito constante igual a entre o eixo do esmeril e seus mancais.
a) Ache a força que deve ser aplicada tangencialmente à extremidade do eixo da manivela de de comprimento para acelerar a roda do esmeril desde zero até em . b) Depois que o esmeril atinge a velocidade de , qual é a força tangencial que deve ser aplicada à extremidade da manivela para manter a velocidade angular constante de ?
c) Quanto tempo o esmeril levaria para reduzir sua velocidade angular de até zero quando a única força atuante for apenas a força de atrito nos mancais?
Passo 1
Eaee, belezinha?? Bom... O enunciado nos diz que um esmeril de é um disco sólido de diâmetro igual a .
Você comprime um machado sobre a periferia com uma força normal de , como mostra a figura abaixo:
O coeficiente de atrito cinético entre a lâmina e a pedra do esmeril é igual a , e existe um torque do atrito constante igual a entre o eixo do esmeril e seus mancais.
Queremos calcular a força que deve ser aplicada tangencialmente à extremidade do eixo da manivela de de comprimento para acelerar a roda do esmeril desde zero até em .
Para isso, precisamos saber que:
Onde é o torque, é o momento de inércia e é a aceleração angular.
Para esse passo não ficar muito grande, depois vou apresentando o que as outras alternativas estão pedindo, ok? 😉
Passo 2
Para resolver a letra a), vamos aplicar para o movimento do esmeril.
Como existe uma rotação, consideraremos que ela é positivo e que produz um torque
onde (onde é a força de atrito, é o coeficiente de atrito, é a força normal e é o braço de alavanca).
Logo,
O momento de inércia será .
Repara que , porque o diâmetro é . Então
Passo 3
Aplicando a fórmula do torque,
Este torque deve ser a soma da força aplicada e dos torques de atrito opostos.
Passo 4
Na letra b), queremos a força tangencial que deve ser aplicada à extremidade da manivela para manter a velocidade angular constante de depois que o esmeril atinge a mesma velocidade.
Para manter a velocidade angular constante,
Passo 5
Na letra c), queremos calcular o tempo que o esmeril levaria para reduzir sua velocidade angular de até zero quando a única força atuante for apenas a força de atrito nos mancais.
Bom... Como a única força atuante é a de atrito, utilizaremos somente o torque.
Assim, o tempo necessário, será
Dessa forma, substituindo os valores, temos:
Resposta
- .
- .
- .