Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 48
A distância mínima de parada para um carro que trafega a é , o que inclui a distância percorrida durante o tempo de reação de do motorista.
- Qual é a distância mínima de parada para o mesmo carro se ele estiver a .
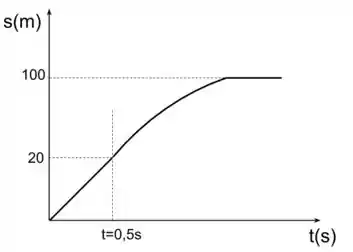
- Trace o gráfico da posição versus tempo para o movimento do carro do item anterior. Considere que ele se encontra em quando o motorista vê pela primeira vez a situação de perigo à sua frente, a qual exige uma parada rápida.
Passo 1
Se liga! O exercício nos fornece informações suficientes para que possamos achar a desaceleração máxima do carro.
Precisamos levar em consideração o tempo que no tempo antes de acionarmos o freio, seguimos com velocidade constante. Se queremos a distância percorrida neste intervalo, precisamos usar a função horária da posição para o movimento retilíneo uniforme.
Considerando que no instante inicial a posição é ZERO, temos
Agora só precisamos substituir os valores
Na configuração a distância total é de , sendo assim, a partir do instante em que o freio é acionado, o carro ainda percorre uma distância de .
Passo 2
Agora, usando a equação de Torricelli, podemos achar a desaceleração máxima do carro
Passo 3
Agora vamos resolver o item (a). Quando a velocidade muda para , a distância percorrida até o freio ser acionado é
E a distância percorrida pelo carro a partir do instante em que o freio é acionado pode ser calculada usando novamente a equação de Torricelli
Então a distância mínima é a soma
Passo 4
O item (b) só precisamos montar o gráfico.
