Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.10 - Ex. 67
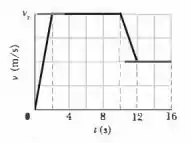
Que distância percorre em um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por
Passo 1
Para começar vamos lembrar a definição de deslocamento:
,
sem esquecer que a integral é a área da função que estamos integrando.
O exercício nos deu o gráfico da velocidade. Então, para calcular o deslocamento, ou distância percorrida, pelo corredor em (), basta calcularmos a área do gráfico de até .
Para resolução de problemas como este, o macete é separar o gráfico em figuras, as quais as fórmulas de área são conhecidas. As fórmulas que você precisa saber para resolver este exercício são:
Passo 2
Para esta questão, vamos calcular a área de quatro figuras, sendo dois retângulos, um triângulo e um trapézio:
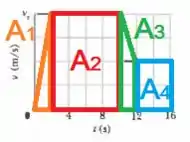
Primeira divisão (triângulo laranja):
Segunda divisão (retângulo vermelho):
Terceira divisão (trapézio verde):
Quarta divisão (retângulo azul):
Portanto, para encontrar o deslocamento do corredor em , somamos as áreas calculadas acima: