Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 109
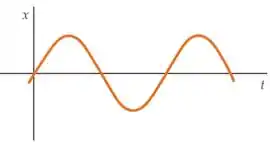
A figura mostra um gráfico de em função de para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo ) de (a) como função de , e (b) como função de . (c) Use os esboços para comparar qualitativamente o(s) tempo(s) no(s) qual(is) o objeto está mais distante da origem ao(s) tempo(s) em que sua rapidez é máxima. Explique porque esses tempos não são os mesmos. (d) Use os esboços para comparar qualitativamente o(s) tempo(s) em que o movimento é mais rápido ao(s) tempo(s) quando sua aceleração é máxima. Explique porque esses tempos não são os mesmos.
Passo 1
(a) Aqui estamos falando apenas de um esboço qualitativo, até porque o gráfico do enunciado nem tem escalas nos eixos.
Como podemos usar o gráfico da posição para encontrar o da velocidade? É só lembrar da seguinte relação:
Ou seja, queremos simplesmente o gráfico da derivada daquela função! Uma forma bem fácil de fazer isso é perceber que a função no enunciado é senoidal:
Sabemos que se trata de um seno, e não de um cosseno, porque . E os valores das constantes e não importam, já que estamos fazendo apenas um esboço.
E desenhando isso no mesmo intervalo para o eixo horizontal:
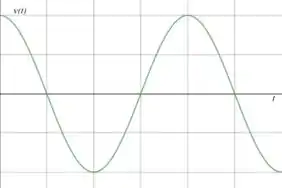
Perceba que, assim como no gráfico do enunciado, nós representamos exatamente um período de onda e meio no eixo horizontal. Ou seja, estamos lidando com o mesmo intervalo de tempo.
Passo 2
(b) Agora para falar da aceleração só precisamos derivar por uma segunda vez:
E podemos continuar ignorando o valor das constantes. Agora vamos voltar para uma função senoidal, mas com o sinal trocado:
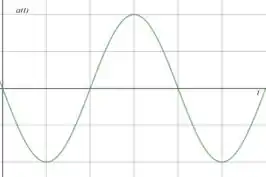
Passo 3
(c) Agora vamos pensar no seguinte: o que acontece com a velocidade nos pontos onde a partícula está a uma distância máxima da origem?
Bom, olhando para o gráfico da posição, vemos que a distância em relação à origem quando a partícula está prestes a inverter o sentido do seu movimento e voltar.
Acontece que nesses pontos a velocidade é nula, justamente para permitir essa inversão!
Passo 4
(d) Olhando para os gráficos, vemos que os picos da velocidade correspondem aos pontos em que a partícula (no gráfico da posição) está passando pela origem, e que nesses pontos, a aceleração é nula.
A aceleração é máxima nos pontos em que a velocidade está sendo reduzida a zero para que a partícula possa mudar de sentido e continuar oscilando.
Resposta
(a) Ver gráfico.
(b) Ver gráfico.
(c) A velocidade é nula nos pontos mais distantes da origem.
(d) A aceleração é máxima nos pontos em que a velocidade é nula, pois está sofrendo uma inversão de sentido.