Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 40.Exercícios - Ex. 14

Passo 1

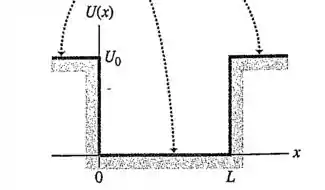
Para uma partícula dentro do poço ( 0 <= x <= L ) psi ( x ) = A c o s ((sqrt(2 m E))/((h // 2 pi)) x) + B s e n ((sqrt(2 m E))/((h // 2 pi)) x) .

Sabemos que o comprimento de onda é dado por:

lambda = (2 pi)/(k)

Como k = (sqrt(2 m E))/((h // 2 pi)) , o comprimento de onda será:

lambda _d e n t r o = (h)/(sqrt(2 m E))

lambda _d e n t r o = (h)/(sqrt(2 m (3 U _o)))

Passo 2

Como fora do poço ( L <= x ) temos o potencial, a número de ondas será k = (sqrt(2 m (E - U _o)))/((h // 2 pi)) , o comprimento de onda será:

lambda _f o r a = (h)/(sqrt(2 m (E - U _o)))

lambda _f o r a = (h)/(sqrt(2 m (2 U _o)))

Passo 3

A razão entre os comprimento de onda será:

(lambda _f o r a)/(lambda _d e n t r o) = ((h)/(sqrt(2 m (2 U _o))))/((h)/(sqrt(2 m (3 U _o))))

(lambda _f o r a)/(lambda _d e n t r o) = sqrt((3)/(2))

Resposta

(lambda _f o r a)/(lambda _d e n t r o) = sqrt((3)/(2))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exercício de Livro
Exercício de Livro
Exercício de Livro
Exercício de Livro
Exercício de Livro