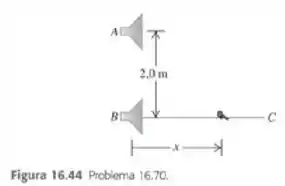
Dois alto-falantes idênticos e estão separados por uma distância de . Os alto-falantes são alimentados por um mesmo amplificador e produzem ondas sonoras com frequência igual a . Considere a velocidade do som no ar igual a . Um pequeno microfone se afasta do ponto ao longo da direção da perpendicular à reta que une o ponto com o ponto (reta indicada na Figura 16.44). a) A que distância do ponto haverá interferência destrutiva? b) A que distância do ponto haverá interferência construtiva? c) Quando a frequência é suficientemente baixa, não existe nenhum ponto da reta com interferência destrutiva. Quão baixa deve ser a frequência para que isso ocorra?

a) Pela imagem, a gente vê que quando uma onda sai do ponto e vai até o ponto ,ela faz o caminho e quando uma onda sai do ponto e vai até o ponto , ela precisa passar pela hipotenusa do triangulo retângulo ABC. Assim podemos escrever a equação de onda destrutiva como:

Sendo o múltiplo do comprimento de onda para cada ponto em que acontece interferência destrutiva

Vamos reescrever a equação para tirar aquela raiz:

Cortando os e isolando :

Agora a gente tem uma equação para sabermos quais os valores de , que é a posição do ponto , ocorrem interferências destrutivas.

Como a questão deu a frequência para a gente, vamos calcular o comprimento de onda:

Substituindo esse valor, o valor de que é a distancia entre as fontes e , e substituindo valores de :

Para :

Para :

Para :

Para :

Para valores maiores, começa a ser negativo.