75. Nos Problemas de 74 a 76 são fornecidas algumas equações que devem ser usadas para resolver um problema. Para cada um deles, você deve
a. Escrever um problema realista para o qual estas equações sejam corretas. Tenha certeza de que sua resposta para o que é pedido no problema seja consistente com as equações fornecidas. b. Fornecer a solução do problema, incluindo uma representação pictórica.
Passo 1
a) Opa! Lá vamos nós! Bora pra mais uma questãozinha sobre Cinemática!
E temos aqui uma questão, provavelmente de movimento relativo pra responder...
Pelas equações que temos do enunciado, o vetor velocidade de módulo na direção tem componente contrária ao da trajetório do corpo. Já na direção , tem o sentido do eixo positivo.
Sendo assim, como a velocidade de está tanto no eixo e ; vamos supor que algum agente externo, é o responsável por esse outro vetor velocidade, de módulo e fazendo com a direção do movimento.
E propomos então, o seguinte problema...
“Um submarino que se move para o leste a vê um navio inimigo a ao norte de seu caminho. O tubo de torpedo do submarino fica preso em uma posição apontando a oeste do norte. O tubo dispara um torpedo com uma velocidade de em relação ao submarino. A que extremo leste ou oeste do navio o submarino deve estar quando dispara?”
Passo 2
b) Bom! Já sabemos que as equações do nosso movimento são as seguintes...
E pra ficar mais compreensível ainda, bora fazer um esboço do panorama do nosso problema...
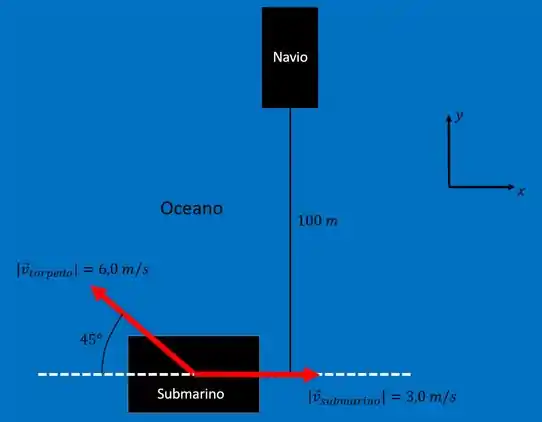
Well! Quando o submarino lança o torpedo, ele precisa percorrer uma distância de , considerando o referencial no eixo , estando a uma velocidade que sabemos ser de...
Sendo assim, tá mais do que na cara que o tempo que o torpedo demora pra atingir o navio é de...
Desse modo, usando a velocidade em , a distância que o submarino deve estar do navio, levando em conta os extremos na horizontal, é de...
Ih rapaz! Deu negativo!
Ora bolas! Se deu negativo... De acordo com o referencial do nosso desenho, é porque o submarino está na extremidade oeste, a uma distância de do alinhamento com o navio, na vertical.
Pronto! Terminamos por aqui!