Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 5.Problemas - Ex. 45
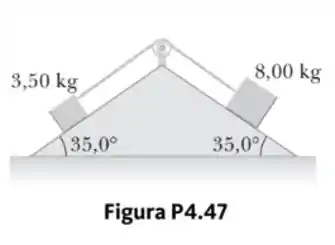
O sistema mostrado na Figura P4.47 (Capítulo 4) tem uma aceleração de módulo . Suponha que o coeficiente de atrito cinético entre o bloco e o plano inclinado seja o mesmo para ambos os declives. Encontre
- o coeficiente de atrito cinético e
- a tensão no fio.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo e bora!
Para o bloco do lado direito , , então:
Passo 2
Para o bloco da esquerda , nos dá:
Resolvendo as equações [1] e [2] simultaneamente temos:
Letra a:
E letra b:
Resposta
Exercícios de Livros Relacionados
42. O bonde mostrado na FIGURA P7.42 desce uma colina de 200m de altura. Além dos freios, o bonde pode controlar sua velocidade puxando um contrapeso de 1.800k g que sobe simultaneamente pelo outro la
37. O bloco de 10,2k g da FIGURA P7.37 é mantido em repouso pela corda sem massa que passa por duas polias sem massa e livres de atrito. Determine os valores das tensões de T 1 a T 5 e o módulo da for
33. O coeficiente de atrito estático entre os dois blocos da FIGURA P7.33 vale 0,60 . O coeficiente de atrito cinético entre o bloco inferior e o piso é de 0,20 . A força F → faz com que os dois bloco
38. O coeficiente de atrito cinético entre o bloco de 2,0k g da FIGURA P7.38 e a mesa vale 0,30 . Quanto vale a aceleração do bloco de 2,0k g ?
36. O bloco de 100k g da FIGURA P7.36 leva 0,6s para chegar ao piso após ser solto a partir do repouso. Qual é a massa do bloco da esquerda?