Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 29
O bloco da Fig. 6-33 pesa e o bloco pesa . Os coeficientes de atrito entre e a rampa são e . O ângulo é igual a . Suponha que o eixo é paralelo à rampa, com o sentido positivo para cima. Em termos dos vetores unitários, qual é a aceleração de se está inicialmente (a) em repouso, (b) subindo a rampa e (c) descendo a rampa?
Passo 1
Belezera pessoal, vamos iniciar essa questão fazendo o diagrama de corpo livre dos dois blocos, partindo da primeira suposição que ambos permanecem em repouso. Sendo assim:
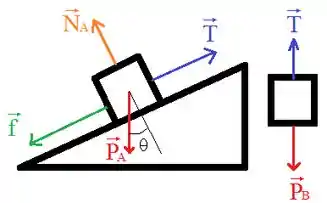
Onde representa a tração na corda, e são as forças normal e peso do bloco respectivamente, enquanto é a força peso do bloco . Já a força é a força de atrito que atua sobre o bloco .
Passo 2
Como estamos supondo que os blocos permanecem em repouso, quer dizer que tração no fio que atua sobre o bloco é grande o suficiente para manter o bloco para no ar, tal que:
Já para o bloco , a tração também tem que ser grande o suficiente para manter o bloc em repouso, de forma que o somatório das forças no eixo da rampa tem que ser nulo:
Então como :
Isolando e substituindo os valores dado na questão:
Logo:
Portanto a força de atrito que mantém os blocos em repouso, possui magnitude .
Passo 3
Mas agora a gente pode calcular a magnitude da força de atrito estático, dada por:
Pra isso, podemos lembrar que a força normal que atua sobre o bloco é dada como:
Sendo assim:
Portanto, a força de atrito estático máximo, será:
E sendo assim, podemos perceber que o módulo da força de atrito estático que atua sobre o bloco é superior ao módulo de atrito cinético que estaria atuando sobre o bloco em caso de inicio de algum movimento. Senso assim, o sistema naõ entra em movimento, os corpos esão em repouso com aceleração nula:
Passo 4
Quando estamos considerando o bloco subindo a rampa, precisamos lembrar que a força de atrito é sempre contrária ao movimento e, portanto, ela apontará para baixo do plano inclinado. Além disso, como o bloco está em movimento, estamos tratando agora da força de atrito cinético que pode ser calculada por:
Só que agora, no eixo da rampa temos que o corpo entrará em movimento, afinal ele está subindo a rampa. Dessa maneira, temos que o somatório das forças que atuam nesse eixo não pode ser nula, nos dando uma celeração resultante , tal que;
O mesmo acontece para o bloco , só que ao contrário do bloco , sua aceleração pe negativa, afinal ele vai estra caindo, de maneira que o somatória das força será:
Substituindo na equação da rampa:
Logo:
Isolando :
Lembrando que podemos obter as massas de cada bloco, dividindo a força peso pela gravida, sendo assim, temos que:
Logo:
Portanto, como medimos a aceleração do bloco que se movimenta apenas no eixo , teremos que:
Mas caso fosse expressar a aceleração do bloco , ela teria a mesma magnitude, só que com sentido e eixo trocados.
Passo 5
Note que fizemos tudo no passo anterior até a equação da aceleração de maneira algébrica. Dessa forma, ao pensarmos no bloco descendo, somente a força de atrito vai mudar de sentido e vai passar a apontar para cima do plano inclinado, as demais forças permanecerão onde estão. Assim, podemos aproveitar a trocando o sinal da força de atrito:
Sendo assim:
Mas ai tu me pergunta, poxa quando o bloco subia e quando o bloco descia a aceleração era negativa, comassim?!?!?!
Mas calma lá jovem mancebo, porque isso quer dizer apenas que quando ele subia a rampa sua velocidade era positiva, e quando ele descia sua velocidade era negativa, mas em ambos os caso nós tínhamos a força peso do bloco A puxando ele para baixo da rampa, ela sempre foi a maior força atuando sobre o sistema. De maneira que por mais que sua velocidade começasse positiva ou negativa, a aceleração que essa força pessoa gerava, sempre iria fazer o bloco A voltar a descer a rampa!!
Resposta
- ;
- ;
- .