Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 31
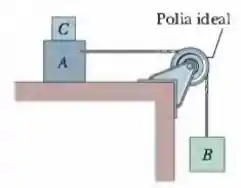
Na Fig. 6-34, os blocos e pesam e , respectivamente. (a) Determine o menor peso do bloco que evita que o bloco deslize, se entre e a mesa é . (b) O bloco é removido bruscamente de cima do bloco . Qual é a aceleração do bloco se entre e a mesa é ?
Passo 1
Show de bolinha pessoal, podemos começar a questão analisando os diagramas de corpo livre para cada um dos blocos, sejam eles:
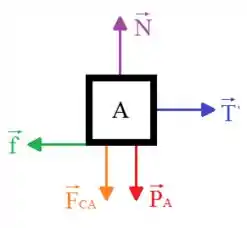
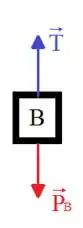
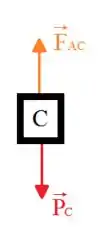
Como os blocos estão em repouso, quer dizer que as forças que atuam sobre eles estão em equilivrio, de forma que o somatório delas em cada bloco sempre vai ser igual a , isto é, os blocos não possuem aceleração. Sendo assim, olhando para o bloco , no eixo temos que:
Já no eixo :
Agora para o bloco , temos que no eixo :
E para o bloco :
Pela terceira lei de Newton, podemos afimar que e, como a polia é ideal, . Além disso, é preciso lembrar que quando consideramos a iminência do movimento estamos falando da que pode ser calculada usando a seguinte relação:
Passo 2
Agora, vamos determinar a normal usando a equação abaixo:
Isolando :
Como vimos que , então:
Podemos então calcular a substituindo a força normal, tal que:
Passo 3
Por fim, temos que:
E como e , então:
Isolando o :
Substituindo os valores dado no enunciado:
Portanto, o menor valor do peso de deve ser .
Passo 4
Ao tirar o bloco bruscamente, o valor de se reduziria a zero e, portanto, a normal seria:
Sendo assim, a força de atrito será:
Substituindo o valor da normal calculado acima, podemos determinar a força de atrito que atua sobre o bloco :
Passo 5
Para determinar o valor de , devemos devemos lembrar que os blocos não estão mais em equilíbrio, de maneira que o somatório das forças gera uma aceleração resultante, tal que:
De maneira análoga, para o eixo do bloco :
Isolando o na equação acima:
Jutando as informações:
Isolando :
Lembrando que podemos descobrir a massa e dividindo as forças pela gravida, tal que:
Logo:
Portanto, ao remover bruscamente o bloco o bloco terá uma aceleração de módulo .
Resposta
- ;
- .