Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 54

Dois capacitores, um com capacitância de e o outro com capacitância de são, primeiramente, descarregados e, então, conectados em série. A seguir, a combinação em série é conectada aos terminais de uma bateria de . Depois, eles são cuidadosamente desconectados de maneira a que permaneçam carregados, e, então, conectados um ao outro novamente placa positiva à placa positiva e placa negativa à placa negativa.

(a) Determine a diferença de potencial em cada capacitor depois que eles foram conectados novamente.

(b) Determine a energia armazenada nos capacitores antes de eles terem sido desconectados da bateria e determine a energia armazenada depois de eles terem sido conectados novamente.

Passo 1

Cara... Primeiramente os capacitores em série são conectados a uma fonte de , o que faz com que os capacitores se recarreguem de modo que aparece uma tensão de em cima deles (em série)...

Sabemos que em série, a carga que aparece em cima de um capacitor é a mesma carga que aparece em cima do outro capacitor. Quanto a tensão que surge em cima de cada um é e ...

Mas claro...

Para encontrar e , podemos usar o fato de que a carga em cima de cada um deles é igual, então...

Conhecendo e , e com essas duas equações nós podemos determinar o valor de e .

Depois disso, os dois capacitores são então conectados um ao outro...

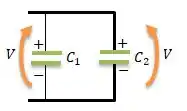
Bem... Repare então que uma placa vai tender a neutralizar a outra fazendo então surgir uma corrente no circuito. A corrente só vai parar quando as tensões se igualarem a nos dois ramos.

Na letra A, teremos que encontrar essa tensão, saca?

Passo 2

OK! Bem confuso, neh? Vamos por partes! Vamos determinar as tensões que esses capacitores tinham antes dos capacitores se conectarem...

Como vimos no passo anterior, basta utilizarmos essas duas equações...

Como e ...

Então...

E então . Saca?

Passo 3

BELEZA! Mas isso foi antes deles se conectarem. Agora imagina esses dois capacitores se conectando um ao outro...

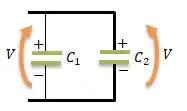
Repare que a placa positiva está conectada a placa positiva (como foi instruído no enunciado).

CARA! Assim que esses dois capacitores se conectarem, como eles possuem diferentes tensões, vai surgir no circuito uma corrente elétrica para equilibrar as cargas em cada placa. A corrente só vai parar de circular quando as tensões em cima dos capacitores estiverem iguais!

POW! Sabemos que a tensão se relaciona com capacitância por , então se as tensões no final do processo atingem , então podemos falar que para os dois capacitores é válida a relação...

Agora... Quem são as cargas e ?

Passo 4

Essas são as cargas que se encontram na placa depois de muito tempo que os capacitores se encontram conectadas.

Como estamos conectando placa positiva com positiva, o total de cargas do sistema depois tem que ser o total de cargas positivas antes da conexão (inicial)...

Pela teoria de capacitores, sabemos que...

Inicialmente no capacitor a tensão é ...

E na placa , a quantidade de cargas nela será exatamente a mesma, já que inicialmente as placas estavam conectadas em série...

Então veja bem, quando as placas são conectadas, após um tempo ligadas, as cargas vão se redistribuir, mas no final das contas o que vai ficar vai ser...