Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 47
Um medidor capacitivo de pressão é mostrado na Figura . Cada placa tem uma área . As placas estão separadas por um material que tem constante dielétrica , espessura e um módulo de . Se um aumento de pressão é aplicado às placas, deduza uma expressão para a variação na capacitância.
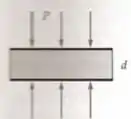
Passo 1
A capacitância sempre pode ser medida por...
Mas repare que aplicando um de pressão ali, vai haver compressão no material!
De acordo com a nossa teoria sobre Deformação e a Lei de Hooke, podemos determinar a variação no distanciamento das placas por...
Onde é a pressão em cima das placas. Então, a partir de agora, vamos deixar de lado a parte do capacitor em si e vamos trabalhar um pouco com essa expressão para determinar compressão (variação de ) do material, pode ser?
Passo 2
Para facilitar, vamos considerar que a pressão inicial era , isto é, no inicio não tinha força nenhuma na placa. De repente surge uma força ...
Onde representa o novo distanciamento das placas.
que aparece, representa a variação da pressão
Passo 3
Então, a capacitância antes da compressão era de...
Depois da compressão ela passa a ser...
De modo que...
Substituindo o resultado do passo anterior...
Então...
Cancelando os termos que dá para cancelar...
Agora substituindo o pela expressão do passo 2...
Simplificando...
Então essa representa a variação da capacitância, saca? Se você quiser, podemos ainda associar como , já que a gente sabe que as duas permissividades estão relacionadas com a constante dielétrica por...
O sinal de menor é porque o é negativo por se tratar de uma compressão, mas a capacitância aumenta com .