Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 63
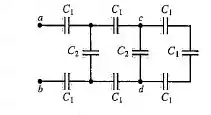
Na figura abaixo, cada capacitância é igual a e cada capacitância é igual a . (a) Calcule a capacitância equivalente do circuito entre os pontos a e b. (b) Calcule a carga dos três capacitores mais próximos de a e de b quando . (c) Determine quando entre a e b a diferença de potencial é igual a .
Passo 1
letra a)
Vamos primeiro calcular a capacitância equivalente entre o 3 capacitores do final
Os capacitores estão em série e possuem a mesma capacitância, logo:
Passo 2
Os capacitores e estão em paralelo:
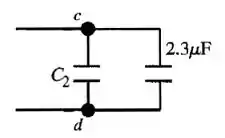
Passo 3
Os capacitores, e estão em série, logo:
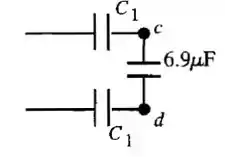
Passo 4
e estão em paralelo então:
Passo 5
Por último (UFA!) temos , e em série
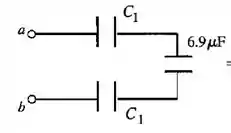
Passo 6
letra b)
Pela última associação que fizemos no passo anterior (, e ), as capacitâncias são iguais e como capacitores em série tem a mesma carga, o potencial deles será o mesmo.
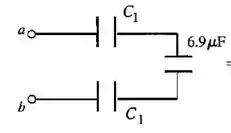
Logo:
Passo 7
Como temos já a capacitância e a voltagem de dos dois capacitores , podemos calcular a carga.
Passo 8
O outro capacitor que precisamos calcular a carga é do . Sabemos que a voltagem , que é a voltagem do capacitor equivalente .
Esse capacitor é a associação do capacitor com o capacitor de .
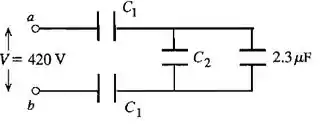
Pelo desenho vemos que e estão em paralelo, logo possuem a mesma voltagem. Sendo assim, .
Passo 9
Como temos já a capacitância e a voltagem podemos calcular a carga.
Passo 10
letra c)
Com os resultados dos itens anteriores podemos fazer um novo desenho.
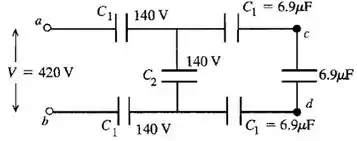
Pelo desenho vemos que é o potencial referente ao capacitor .
Como os três capacitores de estão em série. Isso significa que possuem a mesma carga.
E o que isso no diz????
Mesma carga e mesma capacitância… MESMO POTENCIAL!!
Além disso, está em paralelo com três capacitores . Então:
Resposta
letra a)
letra b),
letra c)