Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 18

Dois discos circulares, espaçados por 0 , 50   m m , formam um capacitor de placas paralelas. A transferência de 3,0 ×   10 2 elétrons de um disco para o outro gera um campo elétrico de intensidade igual a 2,0 ×   10 5   N C . Qual é o diâmetro do disco?

Passo 1

Faaaaaala, galera... Tranquileba??

Temos que o campo elétrico em um disco, então cola comigo que nós faremos juntos.

Precisamos definir o campo elétrico do disco a um ponto com uma distancia z do disco. Assim:

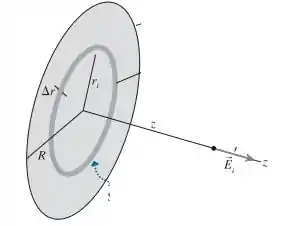
Sabemos pela definição de campo que:

E i = 1 4 π ε 0 ∫ d q r ' 2

Vemos que o campo em x e y se cancelam, logo:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ d q r ' 2 cos ⁡ θ

Sabemos que a densidade de carga é dada por:

η = q A

d q = η   d A = η d π r 2 = η 2 π r   d r

Assim:

E → =   1 4 π ε 0 ∫ η 2 π r d r r ' 2 cos ⁡ θ

Para:

r ' = r 2 + z 2 1 2

E:

cos ⁡ θ = r r ' = r r 2 + z 2 1 2

Assim ficando:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ η   2 π r d r r 2 + z 2   r r 2 + z 2 1 2 = η z 2   ε 0 ∫ r r 2 + z 2 3 2   d

Integrando de 0 ≤ r ≤ R , temos que o campo sobre um disco é:

E → = η 2 ε 0 1 - z R 2 + z 2

Para z ≫ R :

E → = η 2 ε 0 1 - 1 R 2 z 2 + 1

Estando muito próximo do disco R ≫ z de forma que:

E = η 2 ε 0

Sendo de placas paralelas muito próximas, o campo delas se soma, logo:

E = 2 η ε 0 2 = η ε 0

Sendo:

η = Q A

Portanto, o campo elétrico entre dois discos muito próximos é de:

E = Q ε 0 A

Passo 2

Pede-se o diametro, assim:

A = Q E * ε 0

E sabendo que a área de um disco é dada por:

A = π r 2 = π D 2 2

Assim:

D 2 = 4 π Q E * ε 0

Sabendo que:

Q = n * e

D 2 = 4 π n * e E * ε 0

Passo 3

Aplicando os valores:

D = 4 π 3 × 10 2 1.6 × 10 - 19 C 8.85 × 10 - 12   C 2 N m 2 2.0 × 10 5 N C = 1.86   c m

Resposta

O diâmetro D é de:

D = 1.86   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois anéis carregados, com 10 cm de diâmetro cada, são colocados frente a frente e afastados por 20 cm. O anel da esquerda está carregado com - 20n C , e o da direita, com + 20n C . Qual é o campo elé
Dois anéis com 10 cm de diâmetro estão carregados com + 20n C . Qual é a intensidade do campo elétrico no ponto eqüidistante aos dois anéis e;no centro do anel da esquerda?
Dois discos com 10c m de diâmetro são colocados frente a frente e afastados por 20c m . Ambos os discos estão carregados com + 50n C . Qual é a intensidade de campo elétrico no ponto equidistante entr
A intensidade do campo elétrico a 5,0c m de um eletrodo extenso e carregado é de 1 000 N C . Qual é a carga (em nC) sobre um trecho circular do eletrodo com 1,0c m de diâmetro?
Nos Problemas de 62 a 65, uma ou várias equações lhe são fornecidas para a resolução de um problema. Em cada uma das questões, Elabore um problema realista para o qual o conjunto de equações fornecido