Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 11
Dois anéis carregados, com 10 cm de diâmetro cada, são colocados frente a frente e afastados por 20 cm. O anel da esquerda está carregado com , e o da direita, com .
- Qual é o campo elétrico , em módulo e orientação, no ponto equidistante aos dois anéis?
- Qual é a força exercida sobre uma carga de colocada no ponto equidistante?
Passo 1
Faaaaaala, galera... Tranquileba??
Fazendo um desenho do que o enunciado passa nós temos:
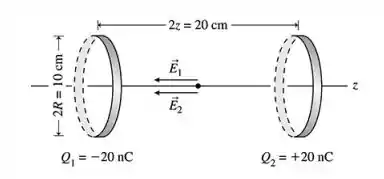
Precisamos determinar o campo elétrico a um ponto da linha z:
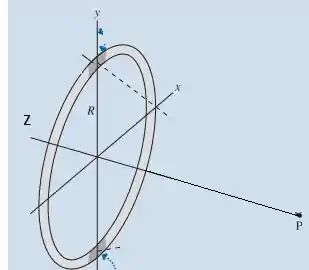
E pede-se então o campo. Bom, sabemos que as componentes em y e x se anulam existindo assim somente componentes em z. logo:
Sendo o modulo da distancia do ponto a um ponto quaisquer do bastão, assim:
E R a distancia ao raio do bastão.
E sabemos também que:
De modo que:
Como o campo elétrico está em Z e não há componente da carga na linha z, z é constante. Logo
E como a soma da carga é a carga:
Este é o campo elétrico para quaisquer dos dois anéis
Passo 2
Suponha que determinamos o campo para , ou seja:
Logo, sendo a componente do anel na direção de -z
O campo em é exatamente igual e positivo também, visto que é positivo, logo elas se somam.
Assim:
E para a esquerda
Passo 3
Para b)
Sabendo que:
Portanto:
Para a esquerda, ou ´para a direita.
Resposta
Para a)
Para esquerda.
Para b)
Para a direita.