Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Questões Conceituais - Ex. 11
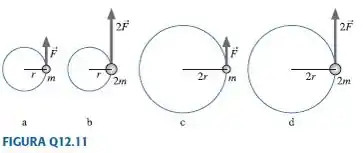
Ordene em sequência decrescente os módulos das acelerações angulares de a na FIGURA Q12.11. Explique o seu ordenamento.
Passo 1
Olá, tudo bem?
Vamos primeiro lembrar como calculamos a aceleração angular em função do torque aplicado:
O braço e alavanca e a força em cada uma das quatro situações formam um ângulo de , então o torque pode ser calculado assim ó:
O momento de inércia de cada conjunto é , onde é a distância do eixo de rotação até a massa , ou seja, o raio da trajetória. Emtão juntando tudo isso a aceleração angular é:
Passo 2
Na situação temos a aceleração:
Na situação temos:
Na situação :
E na última temos:
Passo 3
Beleza até aqui?
Agora é só ordenar em ordem decrescente:
Beleza?
Espero ter ajudado!
Vamos pra próxima?
Resposta
Exercícios de Livros Relacionados
A figura abaixo mostra três discos homogêneos acoplados por correias. Uma correia passa pelas bordas dos discos AeC ; a outra passa por um cubo do disco A e pela borda do disco B . As correias se move
A figura abaixo mostra a variação com o tempo do torque τ que age sobre um disco inicialmente em repouso que pode girar como um carrossel em torno do centro. A escala do eixo τ é definida por τ s = 4
A figura abaixo mostra uma estrutura rígida formada por um aro de raio R e massa m e um quadrado feito de quatro barras finas de comprimento R e massa m . A estrutura rígida gira com velocidade consta
Uma partícula sofre a ação de dois torques em relação à origem: τ 1 → tem módulo de 2 N . m e aponta no sentido positivo do eixo x , τ 2 → tem um módulo de 4 N . m e aponta no sentido negativo do eixo
Uma partícula se move em um plano x y , em torno da origem, no sentido horário, do ponto de vista do lado positivo do eixo z . Em termos dos vetores unitários, qual é o torque que age sobre a partícul