Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 19.Problemas - Ex. 47

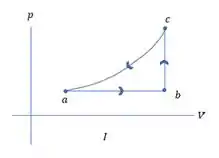
Dois mols de um gás monoatômico ideal passam pelo ciclo a b c . No ciclo completo, 800 J de calor fluem a partir do gás. O processo a b pcprre à pressão constante, e o processo b c , a volume constante. Os estados a   e b apresentam temperaturas T a = 200 K e T b = 300 K .a) Desenhe o diagrama P V   no ciclo.b) Qual é o trabalho W do processo c a ?

Passo 1

Bom galera, vamos usar a primeira lei para relacionar Q t o t a l a W t o t a l para o ciclo.

Calcularemos W a b e W b c e usar o que sabemos sobre W t o t a l para deduzir W t o t a l .

Passo 2

  1. Não nos dizem se a pressão aumenta ou diminui no processo aC. As duas possibilidades para o ciclo é esboçado a seguir:

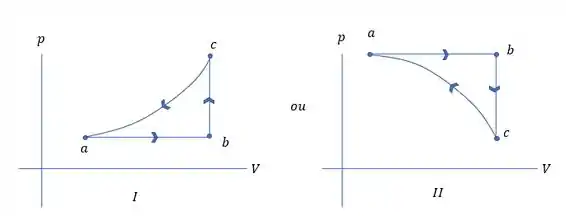
    2. No ciclo   I , o trabalho total é negativo e no ciclo I I , o trabalho total é positivo.

    Para o ciclo, ∆ U = 0 , então Q t o t a l = W t o t a l .

    O fluxo líquido de calor para o ciclo está fora do gás, portanto, o calor Q t o t a l < 0 e W t o t a l < 0 .

    O esboço I está correto.

    Passo 3

W t o t a l = Q t o t a l = - 800   J

W t o t a l = W a b + W b c + W c a

W b c = 0 desde que ∆ V = 0 .

W a b = p ∆ V já que p é constante. Mas como é um gás ideal,

p ∆ V = n R ∆ T

W a b = n R T b - T a = 1660   J

W c a = W t o t a l - W a b = - 800   J - 1660   J = - 2460   J

No processo c a , o volume diminui e o trabalho W é negativo.

Resposta

  2. - 2460   J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade do som num gás (que pode ser tratado como ideal) é 0,683 vezes a velocidade quadrática média das moléculas do gás nas mesmas condições de temperatura e pressão. Qual é o número de átomos
Sejam P C , v C e T C as constantes críticas de um gás de Van der Walls. Mostre que, se exprimirmos a equação de Van der Waals em termos das variáveis reduzidas π = P / P C , ω = v / v C e τ = T / T C
O diâmetro efetivo da molécula de C O 2 é ≈ 4,59 × 10 - 8c m . Qual é o livre percurso médio de uma molécula de C O 2 para uma densidade de 4,91k g / m 3 .
Um feixe molecular de oxigênio, contendo 10 10 m o l é c u l a s / c m 3 é de velocidade média 500m / s , incide sobre uma placa segundo um ângulo de 30 ° com a normal à placa. Calcule a pressão exerc
Um gás é formado de moléculas diatômicas de momento de inércia I = 6 × 10 - 39g ∙ c m 2 . Calcule a velocidade angular de rotação quadrática média de uma molécula do gás em torno de um eixo perpendicu