Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 14.4 - Ex. 19
Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica A área de cada base é , mas em um dos recipientes a altura do líquido é e no outro é . Determine o trabalho realizado pela força gravitacional para igualar os níveis quando os recipientes são ligados por um tubo.
Passo 1
Essa questão é um clássico exemplo de aplicação do Princípio de Pascal. Segundo ele, qualquer alteração de pressão produzida em um fluido em equilíbrio transmite-se integralmente a todos os pontos do fluido e às paredes do seu recipiente. Então, a partir do momento em que os dois recipientes são conectados e os fluidos contidos neles misturam-se formando apenas um fluido, os níveis de líquido em cada um deles igualam-se.
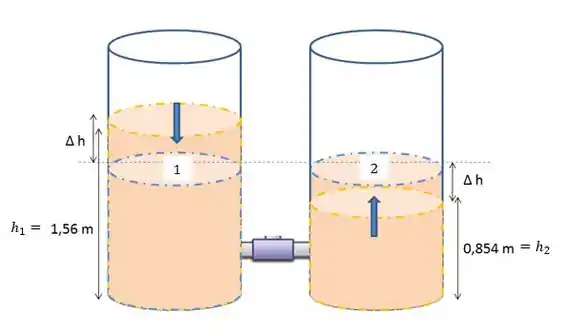
Para que os níveis se igualem é necessário que haja um deslocamento de fluido ao longo do processo, no recipiente 2, que possuía a menor altura de líquido, haverá um aumento na altura do líquido, já no recipiente 1, que possuía a maior altura de líquido haverá uma diminuição nessa altura, como mostra a figura acima.
Passo 2
Agora, vamos entender o que a questão nos pede: o trabalho realizado pela força gravitacional. Em geral, para uma força de módulo constante:
Nesse caso, precisamos calcular o trabalho exercido pela gravidade sobre a massa contida no volume deslocado ao longo do processo.
Passo 3
Pois bem, entendido o conceito por trás do problema, vamos entender porque que as variações de altura dos líquidos em ambos os recipientes são iguais.
Isso ocorre por que de maneira geral, em um problema de vasos comunicantes como esse, as variações de volume em cada recipiente são iguais e dadas por:
E como nesse problema em específico temos que as áreas dos recipientes são iguai: , então:
Passo 4
Ok! . Mas quanto vale essa variação de altura?
Para encontrá-la, basta usarmos o fato de que, no final, os níveis dos líquidos serão os mesmos:
Note que para o recipiente 2, eu somei na altura inicial do líquido e para o recipiente 1 em diminui , por causa do que já comentamos no passo 1, show?
Daí podemos substituir os valores dados na questão e encontramos :
Passo 5
Note, agora, que podemos considerar que a situação final é alcançada quando um volume de líquido dado por:
É deslocado do recipiente 1 para o recipiente 2.
Vimos no passo 2 que temos que calcular o trabalho realizado pela gravidade sobre a massa contida no volume deslocado durante o processo. Então precisamos encontrar a massa associada a esse volume que encontramos.
Para isso vamos utilizar a definição de massa específica:
Então:
Passo 6
Calma que já estamos terminando.
Vamos retornar a equação para o trabalho:
Nós queremos o trabalho da força gravitacional, ou seja, da força peso, então a nossa força é dada por:
Sendo que a massa nós já encontramos:
E o nosso deslocamento é o
Então:
Agora só precisamos substituir os valores dados na questão e o valor de que encontramos:
Obs.: A área eu passei de para para ficar tudo nas unidades do SI.
Fazendo as contas: