Uma esfera maciça homogênea de raio produz uma aceleração gravitacional na superfície. A que distância do centro da esfera está o ponto (a) do lado de dentro e (b) do lado de fora da esfera no qual a aceleração gravitacional é ?

Vamos começar calculando quanto precisamos ir “para dentro” da esfra para atingir a redução da gravidade:

Pela fórmula para o volume da esfera, podemos escrever a massa específica assim:

Vamos substituir isso na fórmula para :

Essa fórmula só vale quando estamos “dentro” da esfera (ou seja, :

Pela fórmula que achamos, temos que a gravidade é igual a uma constante que multiplica o raio:

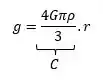
Aí vemos que a aceleração da gravidade fica diretamente proporcional ao raio. Isso quer dizer que se eu dobro o raio, a gravidade dobra, se eu divido o raio por 3 a gravidade também é dividida por três:

Então, utilizando a informação que a questão forneceu:

E essa é a resposta da letra (a).

Agora vamos para a letra (b)

Indo “pra fora” da esfera nós já estamos acostumados. A aceleração segue a fórmula:

Quando ,

E quando qual será o raio?

Vamos igualar :

Pronto!