Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 3
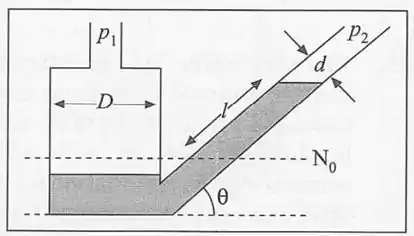
3. O nanômetro de tubo inclinado, utilizado para medir pequenas diferenças de pressão , difere do descrito no problema pela inclinação do ângulo do tubo de diâmetro . Se o fluido empregado é óleo de densidade , com , , escolha para que o deslocamento seja de quando .
Passo 1
Bora lá pro nosso terceiro probleminha nesse maravilhoso e complicado livro de Física.
Esse problema é bastante similar ao exercício do nosso capítulo. Ao olhar a nossa figurinha do enunciado, a primeira coisa que temos de fazer é definir algumas coisas. Por isso, bora chamar a pressão na altura hipotética do lado esquerdo do reservatório de . Desse modo, para o lado direito, obtemos que a pressão exercida pela coluna de líquido na mesma altura é igual a:
Essa é a pressão a partir da linha de referência que começa na altura .
Passo 2
Agora, a questão nos diz que as duas pressões devem se igualar. Desse modo, tem que ser igual a :
Passo 3
Por fim!! Lembra lá dos vasos comunicantes!! Por ele sabemos que Uma variação de volume no lado esquerdo do reservatório deve corresponder a uma mesma variação de volume no lado direito do reservatório... Se considerarmos que o reservatório é cilíndrico, obtemos então, que:
Ótimo! Olha só que beleza! Conseguimos obter em função de . Vamos substituir essa relação na equação que obtivemos no :
Assim, a única coisa que nos resta fazer é obter o valor do ângulo , isolando-o:
Subtituindo os valores numéricos pertinentes, obtemos nossa resposta, igual a: